ある牧場で、牛を１５頭放牧すると、１４日間で食べつくす草が生えています。もし、９頭を放牧すると３５日間で食べつくします。ただし、草は毎日一定の割合で生えるものとし、またどの牛も１日で食べる草の量は同じであるとします。
次の問いに答えなさい。ただし、答えを求めるのに必要な式、考え方などを順序良く書きなさい。
(１)
１日に草が生える量は、牛１頭が１日に食べる草の量の何倍ですか。
(２)
もし、牛２５頭を放牧すると何日間で草を食べつくしますか。
(３)
はじめに牛を７頭放牧して、７日目から何頭か増やしたところ、それが１６日間で草を食べつくしました。何頭増やしたのでしょうか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
牛１頭が１日に食べる草の量を[１]とおくと、
・牛１５頭が１４日間で食べた草の量→[１]×１５×１４＝[２１０]
・牛９頭が３５日間で食べた草の量→[１]×９×３５＝[３１５]
と表すことができます。
このとき、[２１０]は最初から生えていた草の量と１４日間で生えた草の量の合計、そして[３１５]は最初から生えていた草の量と３５日間で生えた草の量の合計なので、次のように消去算を利用して１日に生える草の量の割合を求めることができます。
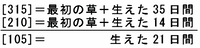
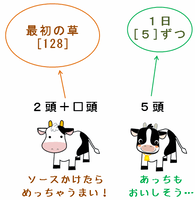
(画像はすべて、クリックすると拡大します)
つまり２１日間に生えた草の量は[１０５]と表せるので、１日に生えてくる草の量は[１０５]÷２１＝[５]になります。
したがって、１日に生える草の量は１頭の牛が１日で食べる量の[５]÷[１]＝５倍になります。
(２)
まずは最初に生えていた草の量の割合を求めます。
[２１０]＝最初に生えていた草の量＋１４日間で生えた草の量
１日に[５]ずつ草が生えるので、１４日間で生えた草の量は[５]×１４＝[７０]となります。
したがって、最初に生えていた草の量は[２１０]－[７０]＝[１４０]と表すことができます。
次の図のように、
牛２５頭のうち５頭は１日[５]ずつ生える草ばかりを食べ、残りの２０頭は最初に生えていた[１４０]の草ばかりを食べると考えます(役割分担)。
上の図の最初の草がなくなったときに草が食べつくされた状態になるので、それにかかる日数は[１４０]÷２０＝７日間になります。
(３)
次の図のように、最初の６日間は７頭のうち５頭が毎日[５]ずつ生えてくる草ばかりを食べ、残りの２頭が最初に生えていた[１４０]の草ばかりを食べます。
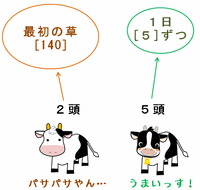
後半の１６日間は、次の図のように最初から生えていた草の残りである[１２８]をさっきの２頭と新入りの牛が食べ、１日[５]ずつ生える草は引き続き５頭が食べることにします。
最初に生えていた草ばかりを食べる２頭の牛が６日間で食べる草の量は[１]×２×６＝[１２]と表せます。
そのとき、最初に生えていた草は７日目にまだ[１４０]－[１２]＝[１２８]残っているのですが、そこからの１６日間でそれもすべて食べつくされます。
このとき、最初に生えていた草の残りを食べる牛たちは、[１２８]の量を１６日間で食べつくしたので、[１２８]÷１６＝８頭いたことが分かります。
ただし、そのうちの２頭は初日からいた牛なので、増やした牛の頭数は８－２＝６頭になります。
PR
