ある３けたの整数があります。この３けたの整数ＡＢＣの一の位の数と百の位の数を入れ替えて、もう１つの３けたの整数ＣＢＡを作ります。
(１)
もとの整数の一の位の数が６と分かっているとき、２つの整数の差を求めると、４９５になりました。もとの整数の百の位の数はいくつですか。
(２)
２つの整数ＡＢＣとＣＢＡをかけたら、答えの一の位の数字が５になりました。ＡとＣの組み合わせは何通り考えられますか。
(３)
２つの整数をかけたら、下の計算のように答えが１１５２４５になりました。十の位の数Ｂはいくつですか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
３けたの整数ＡＢＣの一の位に６をあてはめるとＡＢ６、それをひっくり返すと６ＢＡになります。
また、この問題で求めたいのはもとの整数の百の位(つまりＡ)にあてはまる数です。
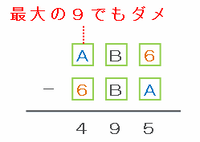
ＡＢ６と６ＢＡの差が４９５なので、「ＡＢ６－６ＢＡ＝４９５」を筆算の図に表すと次のようになります。
しかし、たとえ百の位のＡに最大の数である９をあてはめたとしても、百の位の引き算の答えが４に届くことはないので、２つの数の差を求めるときは「６ＢＡ－ＡＢ６」を計算したことが分かります。
※ 画像はすべて、クリックすると拡大します。
そこで、次のように「６ＢＡ－ＡＢ６」を筆算の図に表してみると、百の位にある６はＡよりも大きいはず(Ａ＞６だと百の位の引き算ができない)です。
つまり一の位でＡから６を引くときには、Ａは６より小さいので、十の位にあるＢから１を借りて「１Ａ－６」を計算したら答えが５になったことが分かります。
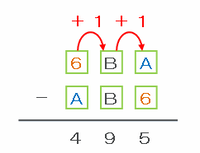
１Ａ－６＝５のとき、５＋６＝１１なので、Ａには１があてはまります。
※ Ｂには０から９までのどれをあてはめてもＯＫです。たとえば「６０１－１０６」でも、「６９１－１９６」でも、引き算の答えは４９５になります。
(２)
「ＡＢＣ×ＣＢＡ」の答えの一の位を５にするためには、ＡＢＣの一の位にあるＣと、ＣＢＡの一の位にあるＡのかけ算が「５×奇数」または「奇数×５」の組み合わせであればＯＫです。
仮にＡ＝５の場合、Ｃは「１・３・５・７・９」からどれか１つを選べばいいので５通りです。
また、Ｃ＝５の場合も、Ａは「１・３・５・７・９」からどれか１つを選ぶので５通りです。
したがって、答えは５×２＝１０通りです、と言いたいところなのですが、それだと(Ａ・Ｃ)＝(５・５)を２回数えてしまっているので、答えは１０－１＝９通りになります。
※ ＡとＣの組み合わせをすべて書き出してみると、(Ａ・Ｃ)＝(５・１)、(５・３) 、(５・５) 、(５・７) 、(５・９) 、(１・５) 、(３・５) 、(７・５) 、(９・５)の９通りです。
(３)
「ＡＢＣ×ＣＢＡ＝１１５２４５」を次のようなかけ算の筆算の図に表してみると、百の位にあるＡとＣをかけた答えがだいたい１１ぐらいになることが分かります。
また、答えの一の位が５なので、一の位にあるＣ×Ａにはさっきの問題で確認した９通りのうちのどれかがあてはまります。
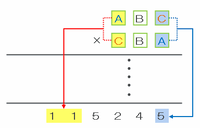
「Ａ×Ｃの答えがだいたい１１」に最も近そうなのは「２×５」なのですが、それだと答えの一の位が５にはなりません(さっき確認したＡとＣの組み合わせ９通りの中にもない)。
かといって「３×５」にしてしまうと１１を超えてしまってアウトなので、百の位のＡとＣには「１×５」があてはまることになります。
※ ＡとＣのどちらかが１、もう一方が５。別にどちらでもＯＫ。
つまり、「１Ｂ５×５Ｂ１」を計算したら答えが１１５２４５になったので、後はＢにあてはまる数を見つければ作業完了です。
とりあえず、「１００×５００＝５００００」だと正しい答えに比べて少なすぎなので、Ｂに最大の数である９をあてはめてみると、１９５×５９１＝１１５２４５でピッタリ賞なので、Ｂには９があてはまります。
※ そもそも「２００×５００」ですら１０００００で正しい答えに届いてないんだから、Ｂに大きい数があてはまるのは当然。
ただ、それだと「適当に見つけただけじゃん」と言われてちょっとムカつくので、ここからは理屈っぽく答えを求めてみます。
「１Ｂ５×５Ｂ１」を次のようなかけ算の筆算の図に表してみると、答えの十の位にある「４」は「１段目のＢ」と「２段目のエ」を足した数であることが分かります。
また、もしＢが偶数なら「１Ｂ５×Ｂ」の答えの一の位は０になるので、下の図の２段目にあるエは０、そしてＢがそのまま４となります。
ただ、１４５×５４１の答えはどう考えても１０万にすら届かないので、Ｂには偶数ではなく奇数があてはまることが分かります。
上の図のＢに奇数があてはまるとき、「１Ｂ５×Ｂ」の答えの一の位は５になるので、図の２段目にあるエは５、そしてＢ＋５＝１４なので、Ｂには１４－５＝９があてはまります。
※ 上の図のＢとエはどちらも最大値が９なので、Ｂ＋エの答えは最大でも１８。エ＝５のとき、Ｂ＋５＝４では式が成立してないので、Ｂ＋５の答えは１４以外あり得ない。
PR
