Ａ、Ｂ、Ｃ、Ｄの４人が、じゃんけん大会をしました。その大会のルールは次のようなものです。
・じゃんけんは１対１で行い、どちらか１人が先に３回勝った時点で終わりとする。
・このとき、３回勝った人がその対戦に勝利したとする。
・全員がそれぞれ、他の３人と一度ずつ対戦する。
すべての対戦が終わったとき、この４人がじゃんけんに勝った回数の合計と負けた回数の合計は、下の表１のようになりました。
※ 画像はすべて、クリックすると拡大します。
(１) Ｂさんは何人に勝利しましたか。また、Ｄさんは何人に勝利しましたか。
次の表２は、この大会における対戦でのじゃんけんの勝敗の様子を一部書き込んだものです。この表にある「３－２」とは、ＡさんがＣさんとの対戦で、ＡさんがＣさんにじゃんけんで３回勝ち２回負けたことを表しています。このとき、ＣさんがＡさんにじゃんけんで２回勝ち３回負けたことになるので、この表に「２－３」が書き込まれています。
(２) 表２のア、イに入る数を答えなさい。
(３) 表２のウ、エに入る数を答えなさい。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
Ｂが自分以外の３人と対戦した結果を次の図のように表してみます。
※ 画像はすべて、クリックすると拡大します。
上の図の□にはそれぞれ０から３までの数があてはまる可能性があるのですが、じゃんけんに勝った回数の合計が９回になるためには、次の図のように３つの□それぞれに「３」をあてはめるしかありません。
つまり、ＢはＡＣＤの３人すべてに勝利した(じゃんけんで３回ずつ勝った)ことが分かります。
ということは、ＤはＢに対してじゃんけんで２勝までしかできなかったことになるので、次の図の紫色の□には、０から２までのどれかがあてはまります。
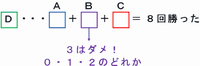
上の図のＢの□に「０」や「１」をあてはめた場合、ＡとＣの□が「３」よりも大きい数になってしまいます。
したがって、Ｂの□には次の図のように「２」をあてはめ、ＡとＣの□にはそれぞれ(８－２)÷２＝３をあてはめることになります。
以上から、Ｂは３人に、Ｄは２人にそれぞれ勝利したことになります。
(２)
表２の「ア－イ」はＢのＤに対する結果があてはまります。
さっきの問題でＢはＤに対して３回勝って２回負けたことが分かったので、ア＝３、イ＝２となります。
(３)
表２の「ウ－エ」はＤのＡに対する結果があてはまります。
ＢはＤに対して「３－２」なので、ＤはＢに対して「２－３」であることが分かります。
また、表１を見るとＢは通算で２回負けているのですが、その相手はどちらもＤでした。つまりＢはＡとＣには１回も負けていないので、ＢはＡとＣに対してそれぞれ「３－０」、ＡとＣはそれぞれＢに対して「０－３」であることも分かります。
ここまで分かったことを表２に書き込んでみると、次のようになります。
ここで上の表２の「？」の部分(ＡのＤに対する結果)に注目してみると、表１からＡは通算で４回勝ったことが分かるので、Ｄに対して４－(０＋３)＝１回勝ったことになります。
また、(１)でＤはＡに勝利した(じゃんけんに３回勝った)ことも分かっているので、ＡはＤに３回負けたことになります。
つまり、上の表２の「？」には「１－３」があてはまるので、「ウ－エ」はその逆である「３－１」になります。
PR
