長さ１２０ｍの普通列車が貨物列車と同じ方向に走っています。普通列車の速さは、はじめ毎時４３.２㎞でした。両列車の先頭が真横に並んでから２分後に普通列車の最後尾と貨物列車の先頭が真横に並びました。その１分後、普通列車は毎時９㎞だけ減速したので、減速してから３分後に普通列車の先頭は貨物列車の最後尾と真横に並びました。ただし、貨物列車の速さは一定です。
次の( )にあてはまる数を求めなさい。
(１)
貨物列車の速さは毎時( )㎞です。
(２)
普通列車が減速したとき、普通列車の最後尾と貨物列車の先頭は( ア )ｍ離れています。また、貨物列車の長さは( イ )ｍです。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは計算しやすいように、普通列車の速さを時速から分速に直しておくと、４３.２×１０００÷６０＝分速７２０ｍになります。
問題文の「両列車の先頭が真横に並んでから２分後に普通列車の最後尾と貨物列車の先頭が真横に並びました」を分かりやすくするため図にしてみると、次のようになります。
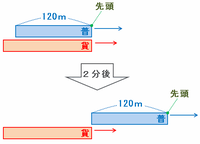
※ 画像はすべて、クリックすると拡大します。
上の図のように、普通列車の先頭はこの２分間で貨物列車の先頭に対して１２０ｍのリードを広げました。
貨物列車の速さを分速□ｍとおくと、普通列車と貨物列車が１分間に進む距離の差は７２０ｍ－□ｍ、そして２分間につく距離の差は(７２０－□)×２という式で表すことができます。
このとき、(７２０－□)×２＝１２０ｍという式ができるので、この式を解いて□を求めてみると、１２０÷２＝６０、７２０－６０＝６６０になります。
つまり貨物列車の速さは分速６６０ｍなのですが、最後にその速さを時速に直すと、６６０×６０÷１０００＝毎時３９.６㎞になります。
(２)の( ア )
次の１分間で普通列車は７２０ｍ、貨物列車は６６０ｍ進みます。
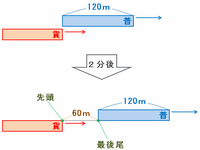
つまり、普通列車は貨物列車に対してさらに７２０－６６０＝６０ｍリードするので、普通列車の最後尾と貨物列車の先頭は、下の図のように６０ｍ離れています。
(２)の( イ )
毎時９㎞を分速に直すと９×１０００÷６０＝分速１５０ｍになるので、減速後の普通電車の速さは７２０－１５０＝分速５７０ｍになります。
貨物列車の速さは分速６６０ｍなので、減速後は貨物列車の方が普通電車を１分間に６６０－５７０＝９０ｍずつ逆転していきます。
つまり、３分間で貨物列車は普通列車よりも９０×３＝２７０ｍ多く進み、普通列車の先頭が貨物列車の最後尾と真横に並んだのですが、そのときの場面を図に表してみると次のようになります。
上の図の？ｍにあたる部分が貨物列車の長さなので、答えは２７０－(６０＋１２０)＝９０ｍになります。
PR
