５円玉、１０円玉、１００円玉が、それぞれたくさんあります。次の問いに答えなさい。
(１)
５円玉と１０円玉を合わせて１００枚使って、その合計金額を８４０円にしたい。５円玉と１０円玉をそれぞれ何枚ずつ使えばよいですか。
(２)
５円玉と１０円玉と１００円玉を合わせて３００枚使って、その合計金額を６１３５円にしたい。５円玉と１０円玉の枚数の比が３：４になるとき、１００円玉は何枚使えばよいですか。
(３)
５円、１０円、１５円、２０円、・・・、９９５円、１０００円という規則で、硬貨を大きな容器に移します。容器の中の合計金額はいくらですか。また、硬貨の枚数ができるだけ少なくなるように移したとき、１０円玉は何枚入っていますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
２種類のものが混ざっていて、合計枚数と合計金額が分かっているので、つるかめ算の公式を利用してそれぞれの枚数を求めることができます。
５円玉枚数を求めたい場合、「もし１００枚が全部１０円玉だったら」と仮定してつるかめ算をスタートすればＯＫなので、その場合の合計金額は１０×１００＝１０００円になります。
実際の合計金額は８４０円なので、つるかめ算の公式を利用して５円玉の枚数を求めると、(１０００－８４０)÷(１０－５)＝３２枚になります。
また、５円玉と１０円玉は合わせて１００枚なので、１０円玉は１００－３２＝６８枚使います。
(２)
５円玉と１０円玉の枚数比は３：４なので、とりあえず５円玉３枚と１０円玉４枚の７枚セットの金額を求めてみると、５×３＋１０×４＝５５円になります。
３種類の硬貨の合計枚数は３００枚、そして３００÷７＝４２余り６なので、
・５円玉と１０円玉の７枚セット→最大で４２セットまで使える
・そのとき、余りの６枚はすべて１００円玉を使う
ことになります。
ただしその場合、合計金額は５５×４２＋１００×６＝２９１０円となり、実際の合計金額に比べて６１３５－２９１０＝３２２５円不足しています。
そこで次の図のように、「５円玉と１０円玉の７枚セット」を「１００円玉７枚」に入れ替えると、１回交換するごとに合計金額は７００－５５＝６４５円ずつ増えます。
※ 画像はクリックすると拡大します。
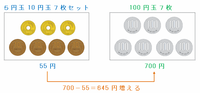
３２２５÷６４５＝５なので、上の図の交換を５回行ったときに３２２５円の不足分が埋まって合計金額は６１３５円になり、その５回の交換作業で１００円玉は７×５＝３５枚増えます。
最初に余りの６枚をすべて１００円玉にした分も含めると、１００円玉は全部で３５＋６＝４１枚になります。
(３)の合計金額の求め方
５円、１０円、１５円、２０円、・・・、９９５円、１０００円の合計金額は、５から１０００までの５の倍数の和を計算すれば求められます、
５から１０００までに５の倍数は１０００÷５＝２００個あるので、合計金額は(５＋１０００)×２００÷２＝１００５００円になります。
(３)の１０円玉の枚数の求め方
たとえば５円から９５円までの間に使われる１０円玉の枚数を確認してみると、
・１０円と１５円→１０円玉がそれぞれ１枚ずつ必要
・２０円と２５円→１０円玉がそれぞれ２枚ずつ必要
・３０円と３５円→１０円玉がそれぞれ３枚ずつ必要
・４０円と４５円→１０円玉がそれぞれ４枚ずつ必要
・５０円と５５円→１０円玉がそれぞれ５枚ずつ必要
・６０円と６５円→１０円玉がそれぞれ６枚ずつ必要
・７０円と７５円→１０円玉がそれぞれ７枚ずつ必要
・８０円と８５円→１０円玉がそれぞれ８枚ずつ必要
・９０円と９５円→１０円玉がそれぞれ９枚ずつ必要
となるので、５円から９５円までに１０円玉は(１＋２＋３＋４＋５＋６＋７＋８＋９)×２＝９０枚必要です。
１０５円から１９５円、２０５円から２９５円、・・・、９０５円から９９５円までの間も１０円玉がそれぞれ９０枚ずつ必要なので、答えは９０×１０＝９００枚になります。
※ 最後のかけ算は、１００円台から９００円台までなら「×９」だけど、５円から９５円までの２０個も含めると「×１０」となる。
１から９までなら指を９本、０から９までなら指を１０本折って数える。
PR
