図１のように、直方体の形をした水そうの底に直方体のおもりを置きました。この水そうに一定の割合で水を入れます。図２のグラフは水を入れ始めてからの時間と水面の高さの関係を表したものです。ただし、立方体は水に浮かないものとします。このとき、次の問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１) 水そうに毎分何㎤の水を入れていますか。
(２) 水を入れ始めてから１６分後の水面の高さは何㎝ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
水を入れ始めてから６分後に水面の高さの増え方が変わるので、ちょうどそのときに水面が立方体のてっぺんまで来たことが分かります。
６分後の水そうを次の図のように真正面から見たとき、水面の高さである８㎝が立方体(図のイ)の一辺の長さになっています。
また、図の水色の部分であるアとウが６分間に入った水の量を表しています。
※ 画像はすべて、クリックすると拡大します。
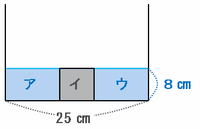
上の図のアイウを合わせた体積は２５×１６×８＝３２００㎤、立方体イの体積は８×８×８＝３２４㎤なので、６分間に入った水の量であるアとウの体積は３２００－５１２＝２６８８㎤になります。
以上から、この水そうには２６８８÷６＝毎分４４８㎤の水が入っています。
(２)
グラフの６分から１６分までの１０分間に入る水の量は、４４８×１０＝４４８０㎤になります。
次の図のように、その水は立方体よりも上の部分にたまるので、まずはその深さを求めてみます。
上の図の緑色の部分の底面積は２５×１６＝４００㎠、体積は４４８０㎤なので、その高さ(図の□㎝)は４４８０÷４００＝１１.２㎝になります。
求めたいのは最初の６分間に入れた８㎝分も含めた水面の高さなので、答えは８＋１１.２＝１９.２㎝になります。
PR
