次の図のように大きい直方体から小さい直方体を切り取った形の水そうがあります。Ａ管、Ｂ管ともに１分間に１６リットルの割合で水が入ります。
※ 画像はすべて、クリックすると拡大します。
はじめＡ管だけをあけ、次にＢ管もあけ、途中でＡ管をしめたところ、水を入れ始めてからの時間と水の深さの関係がグラフのようになりました。
このとき、図のア、イとグラフのウ、エにあてはまる数を求めなさい(式や考え方も書きなさい)。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
【アの求め方】
グラフから、最初の２分間で容器の水の深さは１０㎝になることが分かります。
最初の２分間はＡ管から水が毎分１６リットル＝１６０００㎤の割合で入るので、２分間に入った水の量は１６０００×２＝３２０００㎤になります。
そのとき、容器の中で水が入った部分だけを切り取って図に表すと、次のようなたてア㎝、横４０㎝、高さ１０㎝の直方体になります。
※ 画像はすべて、クリックすると拡大します。
上の図の体積はア×４０×１０＝３２０００㎤という式に表すことができるので、アにあてはまる数は３２０００÷(４０×１０)＝８０になります。
【イの求め方】
グラフから、水の深さが４２－２０＝２２㎝増えるのにかかった時間は、４分２７秒－３分１２秒＝１分１５秒＝１.２５分であることが分かります。
その時間帯はＡ管とＢ管の両方を使って水を入れているので、その１.２５分で容器に入った水の量は１６０００×２×１.２５＝４００００㎤になります。
さっきと同じように、その１.２５分間で水が入った４００００㎤の部分だけを図に表してみると、次のようなたて８０㎝、横イ㎝、高さ２０㎝の直方体ができます。
上の図の体積は８０×イ×２０＝４００００㎤という式に表すことができるので、イにあてはまる数は４００００÷(８０×２０)＝２５になります。
【ウとエの求め方】
４分２７秒からウ分エ秒まではＢ管だけを使って水を入れ、容器の水の深さは５０－４２＝８㎝増えています。
その８㎝分だけを切り取って図に表すと次のような直方体になるので、その容積は２５×８０×８＝１６０００㎤になります。
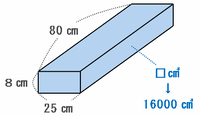
１６０００㎤はＢ管から１分間で入る水の量と等しいので、容器の水の深さが５０㎝になった時間は４分２７秒＋１分＝５分２７秒になります。
したがって、ウには５が、エには２７があてはまります。
【補足 グラフの読み取り方】
問題文に「はじめＡ管だけをあけ、次にＢ管もあけ、途中でＡ管をしめた」とあること、そして容器の幅が途中からせまくなっていることから考えて、次のグラフの①から④の流れには２つのパターンが考えられます。
【パターン その１】
① Ａ管だけを使って水を入れる
② Ｂ管も使い始めたので水の増え方がアップ
③ 容器の幅がせまくなったので水の増え方がさらにアップ
④ Ｂ管だけにしたので増え方ダウン
【パターン その２】
① Ａ管だけを使って水を入れる
② 容器の幅がせまくなったので水の増え方がアップ
③ Ｂ管も使い始めたので水の増え方がさらにアップ
④ Ｂ管だけにしたので増え方ダウン
つまり、②のときに「Ａ管だけ」あるいは「Ａ管とＢ管の両方」を使っているのかによって２通りの流れが考えられるのですが、この問題のアを求めるときには①の条件を、そしてイを求めるときには③の条件を使っているので、特に困ることはありません。
また、グラフの①から③のときの１分あたりの水深の増え方を確認してみると、
① ２分で１０㎝増えた→１分で１０÷２＝５㎝増える
② １.２分で１２㎝増えた→１分で１２÷１.２＝１０㎝増える
③ １.２５分で２０㎝増えた→１分で２０÷１.２５＝１６㎝増える
のようになっています。
このとき、①と②では水深の増え方が１０÷５＝２倍になっていることから、パターン２が正解なら容器の幅は４０㎝からその半分である２０㎝に変わったはずです。
※ 水の量は同じだけど、容器の幅が半分になったから水深の増え方が２倍になった。
しかし実際には、③の条件を使えば容器の幅は２０㎝ではなく２５㎝になったことが分かるので、パターン２は正しくないことが分かります。
PR
