１辺２㎝の正三角形と糸があります。正三角形のＡの位置に糸の端を固定し(図１)、正三角形の周囲に時計回りに糸を巻きつけていくと(図２)、糸のもう一方の端ＰがちょうどＡの位置にきました。
(画像はすべて、クリックすると拡大します)
この状態から、次の(ア)、(イ)の作業を行います。
(ア) 糸をぴんと張った状態に保ったまま、巻きつけてある糸をほどいていきます。
(イ) ほどききったあとも、糸をぴんと張った状態を保ったまま、三角形の周囲に反時計回りに、糸の端ＰがふたたびＡの位置にくるまで巻きつけていきます。
このとき、次の問いに答えなさい。ただし、糸は伸び縮みせず、太さは完全に無視できるものとします。
(１)
糸の長さが６㎝のとき、(ア)、(イ)の作業で、糸の端Ｐが通る経路を、解答用紙にコンパスを用いて、ていねいにかきなさい。経路をかくために使ったその他の線も消さずに残しておくこと。
(２)
糸の長さが３００㎝のとき、(ア)、(イ)の作業で、糸の端Ｐが通る経路は何㎝になりますか。円周率を３.１４として求めなさい。また、求め方も記しなさい。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは(ア)の作図を完成させるために、コンパスを使って次の①から④までの作業をていねいに進めていきます。
① 青い点を中心とした、半径１㎝、中心角１２０度のおうぎ形をかきます。
② 赤い点を中心とした、半径３㎝、中心角１２０度のおうぎ形をかきます。
③ 緑の点を中心とした、半径５㎝、中心角１２０度のおうぎ形をかきます。
④ 紫の点を中心とした、半径６㎝、中心角９０度のおうぎ形をかきます。
これで(ア)の作図は完成なので、次は(イ)の作図を完成させるために、次の⑤から⑧までの作業を同じように進めていきます。
⑤ 紫の点を中心とした、半径６㎝、中心角９０度のおうぎ形をかきます。
⑥ ピンクの点を中心とした、半径５㎝、中心角１２０度のおうぎ形をかきます。
⑦ 水色の点を中心とした、半径３㎝、中心角１２０度のおうぎ形をかきます。
⑧ 黄色の点を中心とした、半径１㎝、中心角１２０度のおうぎ形をかきます。
以上の作業をすべて完成させると、次のような図が完成します。
(２)
【糸をほどく作業のとき】
さっきの①から④までの作業から、糸をほどくときは中心角１２０度のおうぎ形がたくさんできたあと、最後に中心角９０度のおうぎ形が１つできることが分かります。
中心角１２０度のおうぎ形は、半径１㎝→半径３㎝→半径５㎝→・・・のように少しずつサイズが大きくなっていく(すべて奇数)のですが、糸の長さが３００㎝の場合、次の図のように最後は中心角１２０度、半径２９９㎝のおうぎ形のあと、中心角９０度、半径３００㎝のおうぎ形ができて作業が完成します。
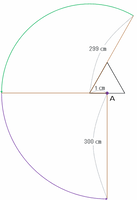
つまり、中心角１２０度のおうぎ形は、半径１㎝から半径２９９㎝までのものが１個ずつでき、さらに中心角９０度、半径３００㎝のおうぎ形が１個だけできます。
【糸をまきつける作業のとき】
糸をまきつけるときは、最初に中心角９０度、半径３００㎝のおうぎ形が１個だけできます(次の図)。
そのあとは中心角１２０度のおうぎ形が半径２９９㎝→半径２９７㎝→半径２９５㎝→・・・のように少しずつサイズが小さくなっていき、最後は半径１㎝のおうぎ形ができて作業が完成します。
つまり糸をまきつけるときも、中心角１２０度のおうぎ形は、半径１㎝から半径２９９㎝までのものが１個ずつでき、さらに中心角９０度、半径３００㎝のおうぎ形が１個だけできます。
というわけで、ここまで分かったことを参考にして孤の長さの合計を求めてみると・・・
【中心角１２０度のおうぎ形の孤の長さの合計】
「１×２×３.１４÷３」から「２９９×２×３.１４÷３」までが全部で２個ずつあるので、とりあえず１から２９９までの奇数の和を求めてみると、(１＋２９９)×１５０÷２＝２２５００になります。
※ 「÷３」は中心角１２０度だから。本当は「×３分の１」と表したいけど、分数はうまく表示できないので(泣)
したがって、中心角１２０度のおうぎ形の孤の長さの合計は、２２５００×２×３.１４÷３×２＝９４２００㎝になります。
【中心角９０度のおうぎ形の孤の長さの合計】
３００×２×３.１４÷４×２＝９４２㎝になります。
以上から、求める長さの合計は、９４２００＋９４２＝９５１４２㎝になります。
PR
