直方体の形をした水そうＡとＢがある。次の図のように、水そうＡの中に水そうＢが入っていて、Ａ、Ｂの真上にそれぞれ蛇口Ｃ、Ｄがある。グラフは、蛇口Ｃ、Ｄからそれぞれ一定の割合で、同時に水を出し始めたときの、時間と水そうＡの水の深さの関係を表している。水そうＢの底面の面積は２１０㎠、深さは６０㎝である。
※ 画像はすべて、クリックすると拡大します。
・蛇口Ｄからは、１分間に( )㎤の水が出ている。
・水そうＡの底面の面積は( )㎠である。
ただし、水そうの厚みは考えない。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
蛇口Ｄから最初の９分間に出た水の量は、水そうＢの容積にあたる２１０×６０＝１２６００㎤です。
したがって、蛇口Ｄから１分間に出る水の量は１２６００÷９＝１４００㎤になります。
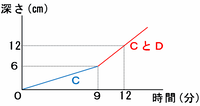
最初から９分間は、水そうＡには蛇口Ｃだけから水が入っていたのですが、その後は水そうＢからあふれた水がＡに流れこんだため、下のグラフのように深さの増え方が急になっています。
※ 画像はすべて、クリックすると拡大します。
このグラフの青い線と赤い線から、
① 蛇口Ｃから９分間→水の深さが６㎝増える
② 蛇口ＣとＤから３分間→水の深さが１２－６＝６㎝増える
③ もし蛇口ＣとＤを９分間使ったら、水の深さは６×３＝１８㎝増える(②を３倍)
という３つのことが読み取れます。
このとき、①と③を次の図のように消去算っぽく計算してみると、
となることから、蛇口Ｄから９分間に入る水の量で、水そうＡは水の深さが１２㎝増えることが分かります。
・水そうＡ→蛇口Ｄから９分間に入る水の量で水の深さが１２㎝増える
・水そうＢ→蛇口Ｄから９分間に入る水の量で水の深さが６０㎝増える(満水になる)
水の量は同じなのにＢの深さがＡの６０÷１２＝５倍になるのは、次の図のように、水そうＡの底面積がＢの５倍だからです。
上の図から、水そうＡの底面積は①＋⑤＝⑥にあたることが分かります。
水そうＢの底面積である①が２１０㎠にあたるので、水そうＡの底面積は２１０×⑥＝１２６０㎠になります。
PR
