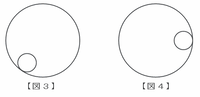
次の図１は、半径４㎝の固定された大円の内側に、半径１㎝の小円板が１点でくっついている図です。この小円板を、大円の内側に沿ってすべらないように転がします。転がし方は、図１の位置を出発し、反時計回りに図２、図３の位置を順に経由して図４の位置に至るまでとします。図１から図４における小円板の位置は、大円を時計に見立てたときの短針の位置で、順に３時、１２時、７時半、３時とします。また、小円板には直径の１つに矢印がかかれており、出発時は図１のように水平に左を向いています。ただし、図２から図４ではこの矢印を省略してあります。このとき、次の問いに答えなさい。ただし、円周率は３.１４とします。
※ 画像はすべて、クリックすると拡大します。
(１)
図１から図２に行くまでに、小円板が転がった大円の円周上の道のりを答えなさい。
(２)
図２、図３、図４における小円板の矢印の向きを、図の小円板の上に書き込みなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
小さい円が図１の「３時」の位置から図２の「１２時」の位置まで反時計回りに動くとき、小さい円は次の図のように大きい円の円周の４分の１だけ進みます。
※ 画像はすべて、クリックすると拡大します。
つまり、求める道のりは半径４㎝の円の円周の４分の１にあたる長さなので、答えは４×２×３.１４×(４分の１)＝６.２８㎝になります。
(２)
大きい円の半径は小さい円の半径の４÷１＝４倍なので、円周の関係も４倍になっています。
PR
