次のような図形があります。今、点Ｐが点Ｂを出発し、辺ＢＣ、ＣＤ、ＤＥ、ＥＡ上を通って点Ａまで動きます。点Ｐは点Ｂを出発して、点Ｅまでは毎秒１㎝の速さで進みます。点Ｅからは速さが変わり、点Ａまで一定の速さで進みます。点Ｂを出発して１５秒後に、三角形ＡＢＰの面積が三角形ＢＣＦの面積と等しくなりました。次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
点Ｐは辺ＥＡ上を、毎秒何㎝の速さで進みますか。
(２)
点Ｐが辺ＢＣ上を１秒間だけ進むと、三角形ＡＢＰの面積は何㎠だけ増えますか。
(３)
三角形ＡＢＰの面積が９㎠となるのは、点Ｐが点Ｂを出発してから何秒後と何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図の辺ＣＦの長さはＤＥと同じく４㎝、そして辺ＢＦの長さは６－３＝３㎝なので、三角形ＢＣＦの面積は４×３÷２＝６㎠になります。
また、三角形ＢＥＡの面積は６×８÷２＝２４㎠です。
※ 画像はすべて、クリックすると拡大します。
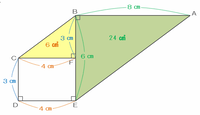
次の図のように三角形ＡＢＰの面積がＢＣＦと同じく６㎠になるとき、三角形ＥＢＰの面積は２４－６＝１８㎠になっています。
また、三角形ＥＢＰとＡＢＰは底辺をそれぞれＥＰ、ＰＡとすると高さが等しくなるので、辺ＥＰとＰＡの長さの比は面積比と同じく１８：６＝３：１になります。
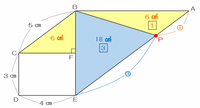
上の図の辺ＥＡの長さは１０㎝、そしてＥＰの長さはＥＡの４分の３にあたるので、１０×４分の３＝７.５㎝です。
点Ｐは次の図の点ＢからＥまでの５＋３＋４＝１２㎝は毎秒１㎝で進むので、点Ｅに到着するのは１２÷１＝１２秒後です。
また、点ＰはＢをスタートしてから１５秒後には、点Ｅから７.５㎝進んだ地点にいました。
つまり、点ＰはＥからの７.５㎝を１５－１２＝３秒間で進んだので、そのときの速さは７.５÷３＝毎秒２.５㎝になります。
(２)
点Ｐは最初の１２秒間は毎秒１㎝で進むので、点Ｂをスタートして５秒後には、次の図のように５㎝先の点Ｃまで進んでいます。
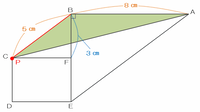
上の図の三角形ＡＢＰは、底辺をＡＢとすると高さは辺ＢＦにあたるので、その面積は８×３÷２＝１２㎠です。
つまり、点ＰがＢを出発してからの５秒間で、三角形ＡＢＰの面積は１２㎠増えたので、１秒間に増える面積は１２÷５＝２.４㎠になります。
(３)
さっきの問題で、点ＰがＣまで進んだときの三角形ＡＢＰの面積が１２㎠となることが分かったので、次の図のように点ＰがＣへ到着するまでのどこかで、三角形ＡＢＰの面積が９㎠となるときがあるはずです。
点Ｐが上の図のように辺ＢＣ上を進むときは、三角形ＡＢＰの面積が１秒間に２.４㎠ずつ増えていくので、ＡＢＰの面積が初めて９㎠になるのは、点ＰがＢを出発してから９÷２.４＝３.７５秒後です。
また、点Ｐが次の図のようにＥを通過してしばらくすると、三角形ＡＢＰの面積が９㎠になるときが訪れます。
この図の三角形ＥＢＰの面積は２４－９＝１５㎠なので、辺ＥＰとＰＡの長さの比は１５：９＝５：３となります。
上の図の辺ＥＰの長さは１０×８分の５＝６.２５㎝、そして点Ｐが辺ＥＡ上を進むときの速さは毎秒２.５㎝なので、三角形ＡＢＰの面積が２回目に９㎠となるのは、点ＰがＥを通過してから６.２５÷２.５＝２.５秒後です。
ただし、この問題は点Ｐが「Ｂを出発してから」の時間を答えなければダメなので、２回目の時間は１２＋２.５＝１４.５秒後になります。
PR
