次の図のような台形ＡＢＣＤがあります。点Ｐは、Ａを出発し時計回りに、点Ｑは、Ｂを出発し反時計回りに、それぞれ一定の速さで動きます。２点Ｐ、Ｑは同時に出発し、出会うたびに、進む方向と速さが入れかわります。
※ 画像はすべて、クリックすると拡大します。
次のグラフは、それぞれ点Ｐ、Ｑについて、「時間」と「底辺ＢＣからの高さ」の関係を表したものです。
(１)
Ｐ、Ｑの出発した時の速さをそれぞれ求めなさい。
(２)
７回目にＰ、Ｑが出会うのは、出発してから何分後ですか。また、それは辺ＡＢ、辺ＢＣ、辺ＣＤ、辺ＤＡのどの辺上で、どの位置ですか。「( )分後、辺( )上で、点( )から( )㎝のところ」という形で答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
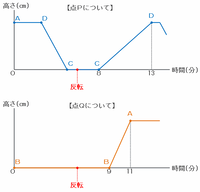
点ＰとＱが進んだ様子を表す次の２つのグラフを見比べてみると、
・頂点Ａを出発して時計回りに進んだ点Ｐの高さがゼロになった→点ＰはＡからＤを通り、Ｃを通過してＢへ向かっていた。
・頂点Ｂを出発して反時計回りに進んだ点Ｑの高さがしばらくずっとゼロだった→点ＱはＣへ着く前にＰと出会って反転した。
ことが分かります。
※ 画像はすべて、クリックすると拡大します。
つまり次の図のように、点ＰとＱは辺ＢＣ上で出会ってお互いに反転し、点Ｐは辺ＣＤの５㎝を１３－８＝５分間で進み、点Ｑは辺ＢＡの４㎝を１１－９＝２分間で進んだことが分かります。
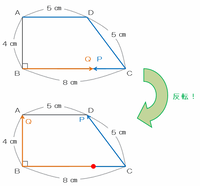
したがって、点Ｐが進む速さは５÷５＝分速１㎝、そして点Ｑが進む速さは４÷２＝分速２㎝であることが分かるのですが、この問題で求めたいのは点ＰとＱが出会って反転する前(スタート時)の速さです。
さっき求めた速さは２つの点が反転して速さが入れかわった後のものなので、２つの点が出発したときの速さは、点Ｐが分速２㎝、そして点Ｑが分速１㎝になります。
(２)
点Ｑの動きを基準にして、２つの点が７回目に出会うまでの時間と場所を求めます。
１回目に出会うのは、次の図のように２つの点が合わせて５＋５＋８＝１８㎝動いたときです。
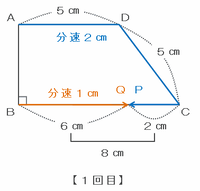
最初は点Ｐが分速２㎝、点Ｑが分速１㎝で進むので、その２つの点が合わせて１８㎝動くのにかかる時間は１８÷(２＋１)＝６分です。
したがって、点Ｑはスタートから６分後に頂点Ｂから反時計回りに１×６＝６㎝進んだ地点にいます。
２回目に出会うのは、２つの点が合わせて台形の１周分の距離にあたる４＋５＋５＋８＝２２㎝進んだときです。
今度は点Ｐが分速１㎝、点Ｑが分速２㎝で進むので、その２つの点が合わせて２２㎝動くのにかかる時間は２２÷(１＋２)＝３分の２２分です。
また、３回目に出会うときも次の図のように２つの点が合わせて２２㎝動くので、やはり３分の２２分かかります(ただし、２つの点の速さはまた入れかわっています)。
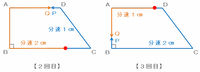
以上のことから点Ｑの動きをまとめてみると、
・１回目に出会うまで→反時計回りに分速１㎝で６分間進む。
・２回目に出会うまで→時計回りに分速２㎝で３分の２２分間進む。
・３回目に出会うまで→反時計回りに分速１㎝で３分の２２分間進む。
となることから、点Ｑは次の表のように、「偶数回目の出会い→時計回りに分速２㎝で３分の２２分間進む」、「奇数回目の出会い→反時計回りに分速１㎝で３分の２２分間進む」という動きをくり返すことが分かります。
※ ただし、１回目の出会いのときだけは例外。
この表を利用して、時計回りと反時計回りに進んだ距離の合計をそれぞれ求めてみると、
・時計回り→分速２㎝で３分の２２分ずつ３回進んだので、２×３分の２２×３＝４４㎝
・反時計回り→１回目は分速１㎝で６分、残りの３回は分速１㎝で３分の２２分ずつ進んだので、１×６＋１×３分の２２×３＝２８㎝
となることから、点Ｑは次の図のように、出発点である頂点Ｂから時計回りに４４－２８＝１６㎝進んだことが分かります。
また、進んだ時間の合計は「１回目は６分」と「２回目から７回目までは３分の２２分ずつ」なので、６＋３分の２２×６＝５０分です。
以上から、答えは「５０分後、辺ＢＣ上で、点Ｃから２㎝のところ」になります。
※ 「点Ｂから６㎝のところ」でもＯＫです。
PR
