ある工場では、ある製品を毎日同じ量だけＡ、Ｂ２種類の機械を何台かずつ使って仕事をしている。Ａを３台、Ｂを２台使うと３時間２０分で生産が終わり、Ａを２台、Ｂを５台使うと２時間１５分で生産が終わる。
(１)
Ａだけを４台使うと、生産を終わらせるのに何時間何分かかりますか。
(２)
Ａを何台かと、Ｂを９台使い、４５分以内で生産を終わらせるようにしたい。少なくともＡを何台使えばよいですか。
(３)
ある日、Ａを２台、Ｂを２台使って生産を始めた。１時間後、Ａを２台加えてさらに１時間生産を続けたところで、Ａをすべて止めなくてはならなくなった。そこで、Ｂを３台加えて残りの生産を終わらせた。生産を始めてから終わらせるまでに、合計何時間何分かかりましたか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは機械Ａが１分間にできる仕事の量を□、機械Ｂが１分間にできる仕事の量を△とおいて、３時間２０分と２時間１５分でできた仕事の量を式で表してみます。
【その１ Ａを３台、Ｂを２台使った場合】
Ａを３台とＢを２台使うと３時間２０分＝２００分で生産が終わりました。このとき、ＡとＢが２００分でできた仕事の量をそれぞれ式で表してみると、
・Ａ３台で２００分→□×３台×２００分＝□×６００
・Ｂ２台で２００分→△×２台×２００分＝△×４００
となるので、この仕事全体の量は「□×６００＋△×４００」という式で表せます。
【その２ Ａを２台、Ｂを５台使った場合】
Ａを２台とＢを５台使うと２時間１５分＝１３５分で生産が終わるので、こちらもさっきと同じように仕事の量をそれぞれ計算してみると・・・
・Ａ２台で１３５分→□×２台×１３５分＝□×２７０
・Ｂ５台で１３５分→△×５台×１３５分＝△×６７５
となり、この仕事全体の量は「□×２７０＋△×６７５」という式で表せます。
その２つの式を次の図のように並べてみると、□が６００－２７０＝３３０減った代わりに△が６７５－４００＝２７５増えたので、仕事量の合計は結局変わりませんでした。
※ 画像はすべて、クリックすると拡大します。
このとき、上の図の「□×３３０」と「△×２７５」は等しいので、比の内項と外項の積が等しいことを利用すると、□：△＝２７５：３３０＝５：６となります。
つまりＡ１台あたりの１分間の仕事量を⑤とおくと、Ｂ１台あたりの１分間の仕事量は⑥と表せるので、次の図のようにさっきの式の□に⑤、△には⑥をあてはめてみると、どちらの式でも仕事全体の量は５４００になります。
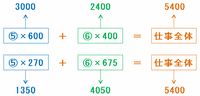
Ａ１台の１分間の仕事量は⑤、それを４台使って□分で５４００の仕事を片づけるのにかかる時間を求めればＯＫなので、「⑤×４台×□分＝５４００」を逆算して□にあてはまる数を求めてみると、５４００÷(５×４)＝２７０分になります。
２７０÷６０＝４余り３０なので、答えは４時間３０分になります。
(２)
Ｂ１台の１分あたりの仕事量は⑥なので、それを９台使って４５分動かすと、⑥×９台×４５分＝２４３０の仕事ができます。
残りの仕事量は５４００－２４３０＝２９７０なので、Ａを□台使って４５分でその仕事を片づける場面を式で表すと、「⑤×□台×４５分＝２９７０」となります。
その式を逆算して□を求めると、２９７０÷(５×４５)＝１３.２台となるので、４５分以内で生産を終わらせるためには１３＋１＝１４台使えばＯＫです。
(３)
まずは最初の１時間＝６０分でできた仕事量を求めてみると、
・Ａ２台の仕事量→⑤×２台×６０分＝６００
・Ｂ２台の仕事量→⑥×２台×６０分＝７２０
となるので、仕事量の合計は６００＋７２０＝１３２０です。
その次の１時間はＡが２台増えて４台になるので、
・Ａ４台の仕事量→⑤×４台×６０分＝１２００
・Ｂ２台の仕事量→⑥×２台×６０分＝７２０
となり、この１時間での仕事量の合計は１２００＋７２０＝１９２０です。
つまり、最初の２時間で１３２０＋１９２０＝３２４０の仕事ができたので、あとは残りの仕事量である５４００－３２４０＝２１６０を片づけるのに、Ｂを２＋３＝５台使ってどれだけの時間がかかるのかを求めてみます。
⑥×５台×□分＝２１６０のとき、□には２１６０÷(６×５)＝７２分があてはまります。
７２分＝１時間１２分なので、最初の２時間も合わせると答えは３時間１２分になります。
PR
