上の図のように半径６cm、円の４分の１の図形ＯＡＢがあります。その円周の一部分であるＡＢを３等分する点をとり、点Ｂに近いほうをＣとします。また半径ＯＢのまん中の点をＤとします。このときぬりつぶした部分の面積は何㎠ですか。ただし、円周率は３.１４として計算しなさい。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック！
大まかに言うと、次の図のおうぎ形全体からアとイの面積を引けば、求めたいウの面積が分かりそうです。
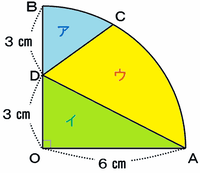
イは単なる直角三角形なので、面積は６×３÷２＝９㎠とすぐ求められるのですが、おうぎ形のニセモノであるアの面積を求めるのはちょっと大変そうですね。
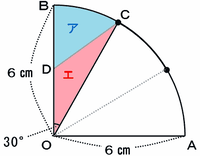
でもアの面積だって、次の図のアとエを合わせた面積(おうぎ形ＢＯＣ)からエの面積を引けば求められます。
点Ｃは孤ＢＡを３等分している点なので、おうぎ形ＢＯＣの中心角は９０÷３＝３０度です。
したがって、おうぎ形ＢＯＣの面積は６×６×３.１４÷１２＝９.４２㎠になります。
あとは上の図の三角形ＣＯＤの面積を求めればＯＫです。辺ＤＯの長さは３cmと分かっているので、高ささえ分かれば答えにたどりつけそうです。
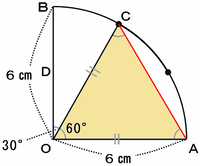
というわけで、三角形ＣＯＤの高さを求めるために、次のように点Ｃから点Ａに向かって補助線をピシッと引いてみます。
上の図の辺ＯＣと辺ＯＡは長さが等しい(どちらもおうぎ形の半径)ので、三角形ＣＯＡは二等辺三角形です。
・・・というのは大ウソですね。
角ＣＯＡが９０－３０＝６０度なので、残りの２つの内角も(１８０－６０)÷２＝６０度ずつ、つまり３つの内角がすべて等しい正三角形になっています。
そこで今度は次の図のように、正三角形ＣＯＡの頂点Ｃから真下に向かって垂線を引いてみると・・・
上の図の赤い垂線ＣＥによって、正三角形ＣＯＡは左右２つの直角三角形に分けられます。
このとき、辺ＯＡも辺ＯＥと辺ＥＡに２等分されるので、辺ＯＥの長さは６÷２＝３cmになります。
そして、この辺ＯＥの長さである３cmは、次の図のように求めたかった三角形ＣＯＤの高さになっているのです。
つまり、三角形ＣＯＤの面積は３×３÷２＝４.５㎠、そして次の図のアの面積は９.４２－４.５＝４.９２㎠になることが分かります。
ここで次の図を使って今までの流れを振り返ってみると、おうぎ形ＢＯＡの面積は６×６×３.１４÷４＝２８.２６㎠、アの面積は４.９２㎠、イの面積は９㎠になっています。
以上から、ウの面積は２８.２６－(４.９２＋９)＝１４.３４㎠になります。
PR
