次の図のように、正三角形ＡＢＣの辺上に４つの点Ｐ、Ｑ、Ｒ、Ｓをとり、正三角形ＡＢＣのまわりの長さを４等分しました。ＡＳの長さは４㎝、ＢＱの長さは１㎝です。このとき、次の各問いに答えなさい。
※ 図形はクリックすると拡大します。
(１)
正三角形ＡＢＣの１辺の長さは何㎝ですか。
(２)
四角形ＰＱＲＳの面積は、三角形ＡＢＣの面積の何％にあたりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図の「辺ＰＡ＋辺ＡＳ」と「辺ＰＢ＋辺ＢＱ」は、どちらも正三角形のまわりを４等分した長さなので、その合計は等しくなっています。
まずは辺ＰＡの長さを①とおき、辺ＰＢの長さの割合を求めてみます。
※ 画像はすべて、クリックすると拡大します。
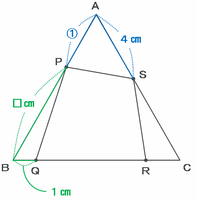
「辺ＰＡ＋辺ＡＳ」と「辺ＰＢ＋辺ＢＱ」の長さを下のような２本の線分図に表して比べてみると、辺ＰＢの長さ(図の□㎝)は、辺ＰＡの長さよりも４－１＝３㎝長いことが分かります。
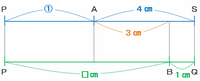
そこで次の図のように、三角形ＡＢＣの辺ＰＡの長さを①、そして辺ＰＢの長さを①＋３㎝と表すことにします。
そのとき、三角形ＡＢＣの１辺である辺ＡＢの長さは①＋①＋３㎝＝②＋３㎝と表すことができます。
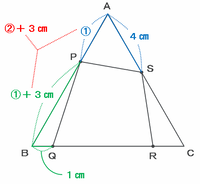
上の図の辺ＰＡと辺ＡＳの長さの合計である「①＋４㎝」は正三角形ＡＢＣのまわりの長さの４分の１にあたるので、それを４倍すれば正三角形ＡＢＣのまわりの長さになります。
したがって、正三角形ＡＢＣのまわりの長さは(①＋４㎝)×４＝④＋１６㎝と表すことができます。
また、辺ＡＰと辺ＰＢの長さの合計である「②＋３㎝」は正三角形ＡＢＣの１辺の長さにあたるので、それを３倍すれば正三角形ＡＢＣのまわりの長さになります。
したがって、正三角形ＡＢＣのまわりの長さは(②＋３㎝)×３＝⑥＋９㎝とも表すことができます。
このとき、「④＋１６㎝」と「⑥＋９㎝」をそれぞれ次のような線分図に表して比べてみると、１６－９＝７㎝が⑥－④＝②にあたることが分かります。
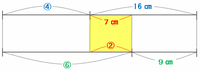
正三角形の１辺である辺ＡＢの長さは「②＋３㎝」なので、答えは７＋３＝１０㎝になります。
(２)
さっきの問題で、正三角形の１辺の長さは１０㎝、そして４等分した長さは７÷２＋４＝７.５㎝になることが分かったので、次の図を使って他の残りの辺の長さも求めてみると、
・辺ＳＣの長さ→１０－４＝６㎝
・辺ＲＣの長さ→７.５－６＝１.５㎝
・辺ＱＲの長さ→正三角形のまわりの長さの４分の１なので７.５㎝
となっています。
四角形ＰＱＲＳの面積は、三角形ＡＢＣの面積から上の図の青色、緑色、オレンジ色の３つの三角形の面積を引けば求められるので、ここからはそれらの三角形の面積の割合を求めてみます。
次の図のように、三角形ＡＢＣは底辺が１０㎝で斜辺の長さも１０㎝なので、面積は１０×１０＝１００と表すことができます。
※ 「÷２」はすべての三角形で省略。
下の図の三角形ＰＢＱとＳＲＣの面積の割合も同じように求めてみると、
・三角形ＰＢＱ→１×６.５＝６.５
・三角形ＳＲＣ→１.５×６＝９
PR
