気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
05/29
Sat
2010
武蔵2010【1】の(1) ☆平面図形・三角形の面積比☆
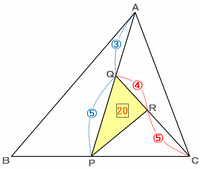
AQ:QP=3:5、CR:RQ=5:4という2つの比を三角形の底辺や高さだと考えて、ひとつひとつの三角形の面積を求めてみます。
例えば下の図の三角形PQRの場合、底辺をQPの5、高さをQRの4だと考えると、面積は5×4=20と表せます。
三角形の面積なのに「÷2」をしない理由については、この記事の下の方にある【補足】を参照してください。
三角形の面積なのに「÷2」をしない理由については、この記事の下の方にある【補足】を参照してください。
※ 画像はすべて、クリックすると拡大します。
【三角形AQCの面積を求める】
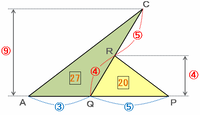
下の図のように辺AQや辺QPが底辺となるように2つの三角形をならべてみると、三角形PQRの面積はさっき求めたように5×4=20、そして三角形AQCは底辺が3で高さが4+5=9なので、面積は3×9=27と表せます。
【三角形RPCの面積を求める】
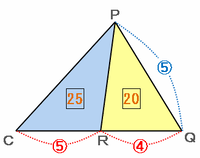
【三角形RPCの面積を求める】
下の図のように辺CRや辺RQが底辺となるように2つの三角形をならべてみると、三角形RPCは底辺が5で高さも5なので、面積は5×5=25となります。
【三角形ABPの面積を求める】
下の図の三角形APCの面積は27+20+25=72、そして三角形ABCの面積は三角形PQRの6倍なので20×6=120と表せます。
したがって、三角形ABPの面積は120-72=48となります。
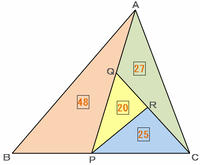
以上から、三角形ABCは下の図のように左右2つの三角形に分けられ、その面積比は三角形ABP:三角形APC=48:72=2:3になっていることが分かります。
また、この2つの三角形は高さが等しいので、底辺である辺BPと辺PCの比も面積比と同じく2:3になっているはずです。
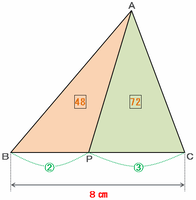
以上から、BPの長さは8×5分の2=3.2㎝になります(比例配分)。
以上から、BPの長さは8×5分の2=3.2㎝になります(比例配分)。
【補足】
「三角形の面積を求めるのになんで÷2をしてないの?」と思ったあなた。試しにすべての三角形で÷2をしてみると次のような感じになります。
・三角形PQRの面積→5×4÷2=10
・三角形AQCの面積→3×9÷2=13.5
・三角形RPCの面積→5×5÷2=12.5
・三角形APCの面積→10+13.5+12.5=36
・三角形ABCの面積→10×6=60
・三角形ABPの面積→60-36=24
以上から、三角形ABPと三角形APCの面積比は24:36=2:3となります。
つまり、「すべて÷2をした場合」と「すべて÷2をしなかった場合」では答えが結局同じになるので、めんどくさければいちいち÷2をしなくてもOKなのです。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
