次の図のような１辺が１０cmの正方形ＡＢＣＤがあります。図においてＥはＢＣのまん中の点です。ＡＢとＧＥは平行で、ＤＨとＡＥは垂直です。次の問いに答えなさい。
(１) 長さの比ＨＦ：ＡＦとＡＦ：ＦＤをそれぞれ最も簡単な整数の比で表しなさい。
(２) 三角形ＤＦＡの面積を求めなさい。
(３) 三角形ＥＦＧの面積を求めなさい。
※ 解説を見たい場合は、下の「解説はこちらから」をクリック！
(１)
問題文から、辺ＡＢと辺ＡＤは１０cm、辺ＢＥは１０÷２＝５cmであることが読み取れます。
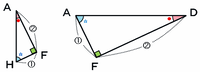
また、この正方形の中には、次の図１のように同じ角度(●、☆、直角)がたくさんあります。
(図形はすべて、クリックすると拡大します)
例えば三角形ＡＢＥのように、３つの内角が●、☆、直角でできている三角形はすべて相似(合同の可能性もある)なので、直角をはさむ２つの辺の長さの比は、ＢＥ：ＡＢ＝５cm：１０cm＝１：２になっているはずです。
そして次の図のように、この問題で求めるＨＦ：ＡＦとＡＦ：ＦＤは、どちらも直角をはさむ２つの辺の長さの比にあたるので、答えはどちらも１：２になります。
(２)
次の図のように三角形ＡＢＥと三角形ＡＨＤを比べてみると、辺ＡＢと辺ＤＡはどちらも１０cm、そして３つの内角は同じなので、この２つの三角形は合同であることが分かります。
したがって、辺ＡＨは辺ＢＥと同じく５cmになり、三角形ＡＨＤの面積は１０×５÷２＝２５㎠だと分かります。
次に三角形ＡＨＤを、底辺がＨＤになるようにかたむけてみると、三角形ＡＨＤは辺ＡＦによって三角形ＨＦＡと三角形ＤＦＡに分けられ、この問題で求めたいのは、右側にある三角形ＤＦＡの面積です。
また、この左右２つの三角形は高さが等しい(辺ＡＦ)ので、辺ＨＦと辺ＦＤの長さの比が面積の比と等しくなります。
そこで、(１)で求めた長さの比であるＨＦ：ＡＦとＡＦ：ＦＤを、次のように連比にしてそろえてみます。
この連比から、ＨＦ：ＦＤ＝１：４であることが分かるので、三角形ＨＦＡと三角形ＤＦＡの面積比も１：４になります。
三角形ＡＨＤの面積は２５㎠、そして求めたい三角形ＤＦＡの面積はその５分の４にあたるので、２５×５分の４＝２０㎠になります。
※ 三角形ＡＨＦの面積は２５－２０＝５㎠です(次の問題で使います)。
(３)
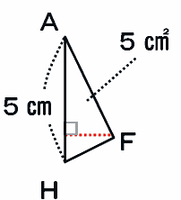
三角形ＡＨＦは面積が５㎠、辺ＡＨの長さが５cmと分かっているので、辺ＡＨを底辺としたときの高さ(次の図の赤い点線)を□cmとおくと、５×□÷２＝５㎠と表せ、□は５×２÷５＝２cmになります。
また次の図のように、三角形ＡＨＦと三角形ＥＦＧは８の字相似になっています。
この図の赤い線＝２cm、ＢＥ＝５cmなので、青い線(三角形ＥＦＧ)の長さは５－２＝３cmです。
つまり、三角形ＡＨＦと三角形ＥＦＧの長さの比は２：３なので、面積の比は２×２：３×３＝４：９になります。
比の４が三角形ＡＨＦの面積である５㎠にあたるので、比の１は５÷４＝１.２５㎠です。
三角形ＥＦＧの面積は比の９なので、１.２５×９＝１１.２５㎠です。
いつもクリックありがとうございます！
PR
