Ａ君は２０から５０までの間にある３の倍数のすべての和を求めようとしましたが、１つの数の十の位と一の位を入れかえて足してしまったため、和が５４だけ大きくなりました。Ａ君は( )の十の位と一の位の数字を入れかえて計算しました。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
３の倍数である元の数の十の位をア、一の位をイとおくと、十の位と一の位の数を入れかえた数は「イア」と表せます。
また、元の数「アイ」の代わりに「イア」を足したら合計が増えたので、
・「アイ」よりも「イア」の方が大きい数である
・「ア」よりも「イ」の方が大きい数である
ことが分かります。
「イア」は「アイ」よりも５４大きいので、「イア－アイ＝５４」の計算を次のような筆算に表すことができます。
※ 画像はクリックすると拡大します。
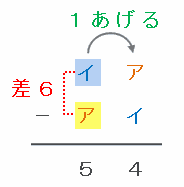
「ア」は「イ」よりも小さい数なので、上の図で一の位にある「ア」から「イ」を引くときには、十の位にある「イ」から１借りてくる必要があります。
その後で十の位にある「イ」から「ア」を引いたら５になったので、「イ」は「ア」よりも５＋１＝６大きいことが分かります。
元の数「アイ」は２０から５０までの間にある３の倍数なので、十の位には２、３、４のいずれかがあてはまります。
そこで、十の位が２、３、４のどれだと３の倍数になるのか調べてみると・・・
・十の位が２のとき・・・一の位は２＋６＝８。２８は３の倍数ではないのでアウト。
・十の位が３のとき・・・一の位は３＋６＝９。３９は３の倍数なのでＯＫ。
・十の位が４のとき・・・一の位は４＋６＝１０。２けたの数にならないのでダメ。
となることから、元の数は３９になります。
PR
