同じ数を３回かけた数の答えは、次のような連続する奇数の和に直すことができます。
２×２×２＝３＋５
３×３×３＝７＋９＋１１
４×４×４＝１３＋１５＋１７＋１９
このとき、次の問いに答えなさい。
(１)
７×７×７を連続する奇数の和の形に直しなさい。
(２)
１７×１７×１７を連続する奇数の和の形に直したとき、その中で小さい方から９番目の奇数はいくつですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
３回かけあわせる数が奇数か偶数かによってちょっとルールが違うので、まずはそこから確認してみたいと思います。
【奇数を３回かけあわせたときのルール】
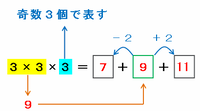
「３×３×３」は「３×３」の答えである９が３個あるということなので、真ん中の数を９にして、その左側には９－２＝７、そして右側には９＋２＝１１を置いてあげれば、次の図のように「７＋９＋１１」という形で９を３個ならべたことになります。
※ 画像はすべて、クリックすると拡大します。
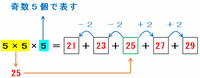
同じように「５×５×５」の場合を考えてみると、「５×５」の答えである２５を５個ならべればＯＫなので、次の図のように真ん中に２５を置き、その左右に連続する奇数を２個ずつならべれば２５が５個あることになります。
【偶数を３回かけあわせたときのルール】
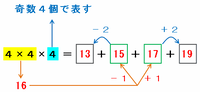
「４×４×４」は「４×４」の答えである１６が４個あるという意味ですが、１６は偶数なので「連続する奇数の和」には使えません。
そこで、まずは１６－１＝１５と１６＋１＝１７を真ん中に置き、１５の左側には１５－２＝１３を、そして１７の右側には１７＋２＝１９を置いてあげれば、「１３＋１５＋１７＋１９」という形で１６を４個並べたことになります。
同じように「６×６×６」の場合を考えてみると、「６×６」の答えである３６を６個ならべればＯＫなので、次の図のように真ん中に３６－１＝３５と３６＋１＝３７を置き、その左右に連続する奇数を２個ずつならべれば３６が６個になります。
さて、ルールを確認したところでそろそろ本題に入ります。
「７×７×７」は「７×７」の答えである４９が７個ある、という意味なので、まずは次の図のように７個の奇数の真ん中に４９を置き、その左側には２ずつ小さい数を、そして右側には２ずつ大きい数をならべていけばＯＫです。
以上から、答えは「４３＋４５＋４７＋４９＋５１＋５３＋５５」になります。
(２)
「１７×１７×１７」は「１７×１７」の答えである２８９が１７個ある、という意味なので、まずは１７個の奇数の真ん中に２８９を置き、その左側には２ずつ小さい数を８個、そして右側には２ずつ大きい数を８個ならべれば完成です。
このとき、上の図のように真ん中の数２８９の左側には奇数が８個ならんでいるので、小さい方から９番目の数は真ん中の数である２８９になります。
PR
