２けたの奇数の和を計算する式「１１＋１３＋１５＋・・・＋９９」を作りました。ところが、１か所「＋」の記号を抜かして４けたの数として計算してしまったため、計算の答えが７９２０となりました。どの数とどの数の間の「＋」の記号を抜かしましたか。なお、この問題は解答までの考え方を表す式や文章・図などを書きなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずは「＋」を１個抜かすとどんなことが起きるのかを、実際の例をもとに確かめてみます。
【２３と２５の間にある「＋」を抜かしてしまった場合】
２つの連続する奇数をＡとＢとおき、次の図のようにＡには２３を、そしてＢには２５をあてはめてみます。
※ 画像はすべて、クリックすると拡大します。
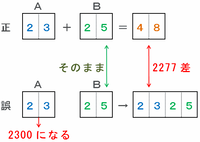
上の図のように、正しく計算を行えば答えは２３＋２５＝４８になります。
しかし「＋」を抜かしてしまうと、Ａにあてはめた２３は２３００として扱われるので、４けたの数２３２５になってしまいます。
このとき、Ｂにあてはめた２５はどちらの計算でもそのまま２５として扱われているため、答えの差である２３２５－４８＝２２７７は、Ａの数を「２３」あるいは「２３００」として扱うのかによって生じていることが分かります。
※ ２３００－２３＝２２７７
正しい計算のときのＡを[１]とおくと、間違った計算のときのＡはその１００倍として扱われるので[１００]と表せます。
つまり、計算後の答えの差である２２７７は、Ａの[１００]－[１]＝[９９]にあたるので、Ａは２２７７÷[９９]＝２３となります。
・・・なんとなく問題の仕組みを理解したところで、いよいよ本題に突入です。
【ここからが本題】
まずは１１から９９までの奇数の正しい和を求めて、正解と計算ミスの答えにどれだけの差があるのかを確認してみます。
１１から９９までの奇数は、全部で(９９－９)÷２＝４５個あります。
※ １から９９までの奇数－１から９までの奇数＝１１から９９までの奇数
このとき、１１から９９までの奇数の和は(１１＋９９)×４５÷２＝２４７５になるので、計算ミスした答えとの差は７９２０－２４７５＝５４４５になります。
ここで次の図のように、連続する２つの奇数をそれぞれＡとＢとおくと、答えの差である５４４５は、Ａにあてはめた２けたの奇数「アイ」が、間違った計算では４けたの数「アイ００」として扱われたために生じたものです。
２けたの奇数「アイ」を[１]とおくと、４けたの数「アイ００」はその１００倍なので[１００]と表せます。
つまり、その割合の差である[１００]－[１]＝[９９]が、答えの差である５４４５にあたるので、Ａにあてはめた奇数は５４４５÷[９９]＝５５だと分かります。
以上から、「＋」を抜かしたのは５５と５７の間になります。
PR
