上から流れる水を左右に分ける装置があります。次の図は、この装置を３個使って２段に組み合わせたものです。装置が左と右に水を分ける比が１：１のときは、入り口から１００㎤の水を流すと、左から２つ目の出口からは５０㎤の水が流れ出ます。
※ 画像はクリックすると拡大します。
(１)
左と右に分ける比が２：１の装置を１０個使って４段に組み合わせます。入り口から１３５㎤の水を流します。一番多く流れるのは、左から何番目の出口で何㎤ですか。
(２)
１０個の装置を使って４段に組み合わせます。入り口から１２５０㎤の水を流したら、一番左の出口からは１６２㎤の水が流れ出ました。左と右に分ける比を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、ア～コの１０個の装置を４段に設置し、一番上にある装置アに１３５㎤の水を入れます。
すると、その水は左右に２：１の割合で流れるので、イには１３５×３分の２＝９０㎤、ウには１３５×３分の１＝４５㎤の水が入ります。
※ 画像はすべて、クリックすると拡大します。
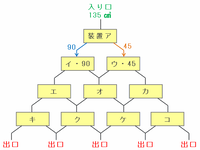
エ～コの装置に流れ込む水の量も同じようにして求めてみると、
・エ→イの３分の２が流れ込むので、９０×３分の２＝６０㎤
・オ→イの３分の１とウの３分の２だから、９０×３分の１＋４５×３分の２＝６０㎤
・カ→ウの３分の１が流れ込むので、４５×３分の１＝１５㎤
・キ→エの３分の２が流れ込むので、６０×３分の２＝４０㎤
・ク→エの３分の１とオの３分の２だから、６０×３分の１＋６０×３分の２＝６０㎤
・ケ→オの３分の１とカの３分の２だから、６０×３分の１＋１５×３分の２＝３０㎤
・コ→カの３分の１が流れ込むので、１５×３分の１＝５㎤
となります(次の図参照)。
したがって、一番多く水が流れるのは左から２番目の出口で、その量は４０×３分の１＋６０×３分の２＝３分の１６０㎤になります。
※ キ～コの中で最も水量が多いのはクで、２番目がキ。左から２番目の出口はクの３分の２とキの３分の１をもらえるんだから、５か所の出口の中では最も水量が多くなる。
(２)
次の図のように、一番左側の出口から出る水の量は、アに入れた水の量を同じ割合で４回比例配分すれば求められます。
※ 例えば左：右＝２：１なら、アに入れた水の量を４回連続で３分の２倍すればＯＫ。
このとき、１２５０分の１６２を約分すると６２５分の８１になるので、その分母と分子を次の図のように４つの同じ数の積で表してみると、□には５が、そして△には３があてはまります。
※ ６２５＝５×５×５×５、そして８１＝３×３×３×３だから。
つまり次の図のように、この問題では装置の中の水が左の出口から５分の３だけ出ていくことが分かったので、右の出口から出ていく水の量の割合は１－５分の３＝５分の２になります。
以上から、左右の出口から出ていく水の量の比は、左：右＝５分の３：５分の２＝３：２になります。
PR
