花子さんの財布には１００円玉３枚、５０円玉２枚、１０円玉１５枚が入っていました。最初のお店で３４０円分の文房具をちょうどの金額を払って買ったら財布には１００円玉( ア )枚、５０円玉( イ )枚、１０円玉( ウ )枚が残りました。次のお店で１５０円のお菓子を買おうとしましたが、財布に入っている硬貨ではちょうどの金額は払えませんでした。このとき、文中の( )にあてはまる数をそれぞれ答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
花子さんの最初の所持金は１００×３＋５０×２＋１０×１５＝５５０円なので、文房具代の３４０円を支払った後の残りは５５０－３４０＝２１０円になります。
そのとき、もし花子さんが５０円玉を１枚でも持っていたら１５０円をちょうど払えてしまうので、まずは次の図のように、文房具を買うときに５０円玉を２枚とも使ってしまいます。
また、文房具代の３４０円のうち「４０円」は１０円玉４枚を使って支払うしかないので、文房具代の残りはあと３４０－１４０＝２００円になります。
※ 画像はすべて、クリックすると拡大します。
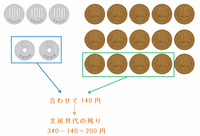
もし文房具代の残り２００円を１００玉２枚で支払うと、１０円玉が５枚以上残って「５０円」が作れてしまうので、次の図のように１００円玉１枚と１０円玉１０枚を使って残りの２００円を支払います。
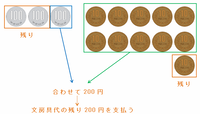
すると、上の図のように残りは１００円玉２枚と１０円玉１枚なので、お菓子代の１５０円をちょうど支払うことができなくなります。
以上から、アには２、イには０、そしてウには１がそれぞれあてはまります。
【補足】
５５０－３４０＝２１０円の中に５０円玉１枚や１０円玉５枚が残っていたらダメなんだから、１００円玉２枚と１０円玉１枚の組み合わせしかありえないじゃん、という大ざっぱな発想でも答えにたどり着けます。
その説明でみんなが理解できるなら話は早いのですが、現実はそれほど甘くないです。
PR
