２つの容器Ａ、Ｂに食塩水が入っています。Ａの食塩水の量はＢの食塩水の量の２倍あり、ＡとＢの食塩水をすべてまぜ合わせると、もとのＢの食塩水の濃度の３倍になります。また、はじめのＡの食塩水に５１０ｇの水を入れると、はじめのＢの食塩水と同じ濃度になります。
(１) はじめのＡとＢの食塩水の濃度の比を求めなさい。
(２) はじめのＡの食塩水の量を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは「ＡとＢを混ぜたらもとのＢの濃度の３倍になった」を天びん図に表してみます。
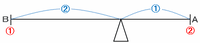
Ａの食塩水の量はＢの２倍なので、Ｂの重さを①とおくとＡの重さは②と表せます。
また、「ＡとＢを混ぜる→Ｂよりも濃い食塩水ができる」ということは、ＡはＢよりも濃いことが分かります。
したがって、次の図のようにうすい食塩水Ｂを左側、濃いＡを右側に書き込んでみると、重さの比はＢ：Ａ＝１：２なので、支点の左右の長さの比は２：１になります。
※ 画像はすべて、クリックすると拡大します。
ＡとＢを混ぜたら濃さがもとのＢの３倍になったのだから、例えば最初のＢの濃さを１％とすると、混ぜてできた食塩水の濃さは１×３＝３％になります。
※ この問題は実際の濃度を求めるわけではないので、「もとのＢ」と「混ぜてできた食塩水」の濃さの関係が３倍なら「２％と６％」でも「３％と９％」でもなんでもＯＫです。
そのとき、下の図の左のうでの長さである②が３－１＝２％にあたるので、右のうでの長さである①は２％÷②＝１％、そしてＡの濃さは３＋１＝４％になります。
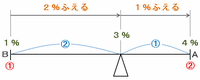
つまり、食塩水Ｂの濃さを１％とするとＡの濃さは４％になるので、濃度の比はＡ：Ｂ＝４：１になります。
【補足】
本当は「もとのＢの濃度を①とおくと、混ぜてできた食塩水の濃さは③と表せるので・・・」っていう流れで解くのが普通なんだけど、それだと「重さの比」「長さの比」「濃さの比」のように比が３種類出てきてややこしいので、もとのＢの濃度を仮に１％とおいて解きました。
でも、解き方自体はどちらにしても同じです。
(２)
さっきの問題でＡとＢの濃度の比が４：１と分かったので、もとの食塩水Ａの濃さを４％、Ｂの濃さを１％として問題を解いていきます。
まずは「はじめのＡの食塩水に５１０ｇの水を入れると、はじめのＢの食塩水と同じ濃度になります」を天びん図に表してみます。
ちなみに５１０ｇの水は「濃さ０％の食塩水」と考え、次の図のように支点の左側に書き込みます。
このとき、上の図の支点の左右のうでの長さを確認してみると、左側は１－０＝１％、右側は４－１＝３％なので、うでの長さの比は左：右＝１：３になっています。
そして重さの比は長さの逆比なので、左右の重さの比は次の図のように左：右＝３：１になります。
つまり食塩水Ａの重さは比の①にあたるので、５１０÷③＝１７０ｇになります。
PR
