ａ、ｂ、ｃという３種類の文字を、左から順に並べます。同じ文字を何度使ってもかまいません。ただし、ａの右隣は必ずｃであり、ｂの右隣も必ずｃであるものとします。この規則を満たす並べ方は、左から１個だけを並べる場合はａ、ｂ、ｃの３通りで、左から２個並べる場合はａｃ、ｂｃ、ｃａ、ｃｂ、ｃｃの５通りとなります。このとき、次の各問いに答えなさい。それぞれ考え方と計算も書きなさい。
(１) 左から３個並べる場合の並べ方は何通りありますか。
(２) 左から４個並べる場合の並べ方は何通りありますか。
(３) 左から７個並べる場合の並べ方は何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
ａ、ｂ、ｃからスタートして３個並べた場合の並べ方を樹形図で表すと、それぞれ次のような図になります。
※ 画像はすべて、クリックすると拡大します。
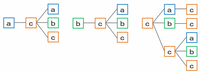
上の図を見れば分かるように、ａから始めた場合は３通り、ｂから始めた場合も３通り、そしてｃから始めた場合は５通りなので、左から３個並べる場合の並べ方は全部で３×２＋５＝１１通りになります。
(２)
さっきの樹形図にもう１個ずつ付け足して、４個並べた場合の樹形図を完成させてみます。
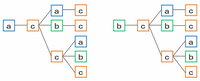
【ａとｂから４個並べる場合の樹形図】
ａとｂから４個並べる場合、並べ方は次の図のようにそれぞれ５通りになります。
【ｃから４個並べる場合の樹形図】
ｃから４個並べる場合、並べ方は次の図のように１１通りになります。
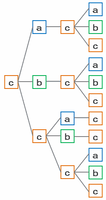
つまり、ａとｂから４個並べる場合は５通りずつ、そしてｃから４個並べる場合は１１通りなので、４個並べる場合の並べ方は全部で５×２＋１１＝２１通りになります。
(３)
さっきの問題で確認した３つの樹形図を、次の図のようにタイプ①～③と名前をつけておきます。
【ａから７個並べる場合の数え方】
とりあえずａから４個目までを樹形図に表すと次のようになるので、たとえば４個目がａならそこからタイプ①をスタートさせると、４個目、５個目、６個目、７個目の４個を並べることができます。
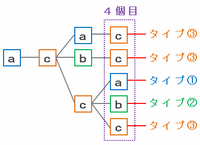
上の図の４個目がｂならそこからタイプ②を、ｃならタイプ③をスタートさせることができるので、ａから始めた場合はタイプ①とタイプ②が１個ずつ、そしてタイプ③が３個できることが分かります。
タイプ①と②はそれぞれ５通りずつ、タイプ③なら１１通りの並べ方ができるので、ａから始めて７個並べる場合の並べ方は、全部で５×２＋１１×３＝４３通りになります。
【ｂから７個並べる場合の数え方】
ｂから４個目までを樹形図に表すと次のようになるので、さっきと同じように４個目からタイプ①～③をスタートさせてみると、ａから７個並べる場合の図とまったく同じになるので、並べ方は全部で４３通りになります。
【ｃから７個並べる場合の数え方】
ｃから４個目までを樹形図に表すと次のようになるので、さっきと同じように４個目からタイプ①～③をスタートさせてみると、タイプ①と②が３個ずつ、そしてタイプ③が５個できます。
したがって、ｃから始めて７個並べる場合の並べ方は、全部で５×６＋１１×５＝８５通りになります。
つまり、ａから始めた場合とｂから始めた場合はそれぞれ４３通り、そしてｃから始めた場合は８５通りなので、７個並べる場合の並べ方は全部で４３×２＋８５＝１７１通りになります。
PR
