気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
04/20
Tue
2010
渋谷教育学園幕張2010【1】 ☆組み合わせ・場合の数☆
下の図のような正三角形の形をした花だんがあり、正三角形の3つの頂点A、B、Cにはそれぞれ1つずつ石がおいてあります。まこと君は、はじめ頂点Aにいます。まこと君は、さいころを1回ふると、自分がいる頂点から花だんのまわりを反時計回り(A→B→C→A→・・・)に歩き、出た目の数だけ先にある頂点に移動します。
※ 例えば、Aにいるまこと君がさいころをふって2の目が出たら、まこと君は2つ先のCへ移動します)。
そして、移動した頂点に石があれば取り除き、石がなければその頂点に石をおきます。
(1)
1回目のさいころの目は1から6までの6通りあるのですが、とりあえず1が出たことにして話を進めていきましょう。
1回目に1が出たとき、まこと君は次の図のようにAからBへ進み、そこで石を取り除きます。
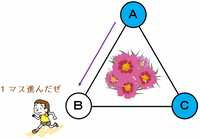
したがって、2回目は次の図の赤い矢印のように3マス進むか、緑色の矢印のようにさらに3マス進んで同じ場所に戻って石を置けば、3つの頂点すべてに石がある状態に戻ります。
つまり、2回目のさいころの目は3または6の2通りあります。
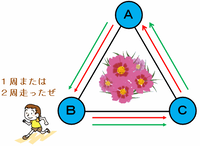
1回目のさいころの目は1から6の6通り、2回目のさいころの目は3または6の2通りなので、求める組み合わせは全部で6×2=12通りになります。
(2)
さっきと同じように、1回目はとりあえず1が出たことにして話を進めると、次の図のようにまずはBの石が取り除かれます。
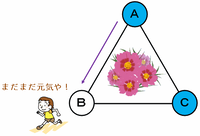
そしてここから先は「B→C→Aの順に取り除くコース」と「B→A→Cの順に取り除くコース」のどちらかに進むことになります。
【B→C→Aの順に取り除くコース】
2回目のさいころでCの石を取り除くためには、次の図のようにBから1マスまたは4マス進む場合の2通りが考えられます。これで残りの石はAだけですね。
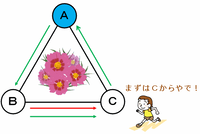
そして3回目でAの石を取り除くためには、やはり次の図のようにCから1マスまたは4マス進む場合の2通りが考えられます。
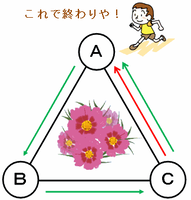
【B→A→Cの順に取り除くコース】
そして3回目でCの石を取り除くためには、次の図のようにAから2マスまたは5マス進む場合の2通りが考えられます。
つまりB→A→Cの順に取り除くコース(1か所目→1個とばし→1個とばし)は、
そして3回目でAの石を取り除くためには、やはり次の図のようにCから1マスまたは4マス進む場合の2通りが考えられます。
つまりB→C→Aのように取り除くコース(1か所目→となり→となり)は、
・1回目のさいころの目→1から6の6通り
・2回目のさいころの目→1または4の2通り
・3回目のさいころの目→1または4の2通り
になるので、全部で6×2×2=24通りあります。
【B→A→Cの順に取り除くコース】
そして3回目でCの石を取り除くためには、次の図のようにAから2マスまたは5マス進む場合の2通りが考えられます。
つまりB→A→Cの順に取り除くコース(1か所目→1個とばし→1個とばし)は、
・1回目のさいころの目→1から6の6通り
・2回目のさいころの目→2または5の2通り
・3回目のさいころの目→2または5の2通り
になるので、全部で6×2×2=24通りあります。
以上から、求める組み合わせは全部で24×2=48通りになります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
