気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
04/21
Wed
2010
雙葉2010【2】 ☆規則性☆
(1)
次の図のように3つの円の中心を結んでみると、一辺の長さが8㎝の正三角形できます。
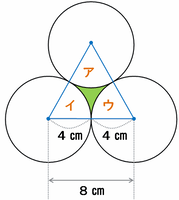
この正三角形の面積は27.71㎠と分かっているので、そこから半径4㎝で中心角60度のおうぎ形3つ(つまり半円)の面積を引けば、緑色の部分の面積が求められます。
半径4㎝の半円の面積は4×4×3.14÷2=25.12㎠なので、求める面積は27.71-25.12=2.59㎠になります。
(2)
まずは円が1段増えるごとに、緑色の部分が何か所ずつ増えていくのかを確認してみます。
・1段のとき→0か所
・2段目まで→1か所(図1)
・3段目まで→1+3=4か所(図2)
・4段目まで→1+3+5=9か所(次の図)
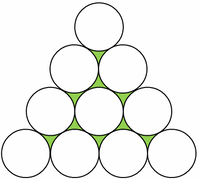
【もうちょっと具体的に説明してみる】
つまり□段目までにある色をぬられた部分の個数は、最初の奇数である「1」から「□-1番目の奇数」までの和になっています。
【もうちょっと具体的に説明してみる】
☆ 3段目までにある緑色の部分の個数
3-1=2なので、最初の奇数である1から2番目の奇数である3までの和を求めればOK。つまり1+3=4か所になります。
☆ 4段目までにある緑色の部分の個数
4-1=3なので、最初の奇数である1から3番目の奇数である5までの和を求めればOK。つまり1+3+5=9か所になります。
つまり、13段目までに色をぬられた部分の個数は、最初の奇数である「1」から13-1=12番目の奇数である「23」までの和を求めればOKなので、(1+23)×12÷2=144個だと分かります。
色をぬられた部分の面積は1か所あたり2.59㎠なので、全部で2.59×144=372.96㎠になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
