ある町の公民館には下の図のように４つの卓球台があります。Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈの８人が対戦を１回するごとに矢印の向きに１つずつ位置を移動しながら対戦をくり返します。最初に８人が図の位置で１回目の対戦を始めたとき、次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
対戦を８回したとき、Ａさんが対戦を２回した人は何人か求めなさい。
(２)
対戦を２０回したとき、Ａさんが１回も対戦できなかった人は何人か求め、その理由をかんたんに説明しなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の問題に備えて対戦相手の規則性を探しつつ、８回目までの対戦相手を図で確認すると次のようになります。
※ 画像はすべて、クリックすると拡大します。
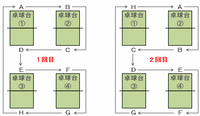
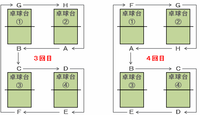
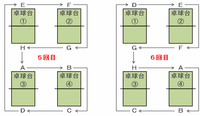
上の４つの図を見れば分かるように、Ａの対戦相手は「Ｄ→Ｂ→Ｈ→Ｆ」が２回くり返されています。
したがって、Ａが対戦を２回したのは全部で４人になります。
(２)
９回目の対戦は１回目とまったく同じ図になるので、Ａの対戦相手はひたすら「Ｄ→Ｂ→Ｈ→Ｆ」のくり返しになります。
したがって、Ａさんが１回も対戦できない相手はＣ、Ｅ、Ｇの３人になります。
【理由の模範解答】
Ａの対戦相手は「Ｄ→Ｂ→Ｈ→Ｆ」のくり返しになるため、残りの３人であるＣ、Ｅ、Ｇとは対戦できないから。
PR
