図のように一辺２ｍの長さの正方形ＡＢＣＤとＣＢＥＦがあります。次のように点Ｐ、Ｑが動くものとします。
① 点ＰはＡを出発してＡ→Ｂ→Ｃ→Ｄ→Ａ→Ｂ→・・・・・・のように正方形ＡＢＣＤの返上を毎秒２ｍの速さで回ります。
② 点ＱはＡを出発してＡＤ上をＤまで動き、ＤからＢにワープしてＢＣ上をＣまで動き、ＣからＥにワープしてＥＦ上をＦまで動き、ＦからＡにワープして戻り、再びＡＤ上をＤまで動きＤからＢにワープしてＢＣ上をＣまで動き・・・・・・(以下繰り返し)。
動く速さは毎秒１ｍです。またワープ(瞬間移動)には時間を要しません。
※ 画像はクリックすると拡大します。
このとき、
(１) ＰとＱが最初に反対向きに動く状態で出会うのは何秒後ですか。
(２) ＰとＱが最初に追いつく形で出会うのは何秒後ですか。
(３) ＰとＱが１０回目に反対向きに動く状態で出会うのは何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
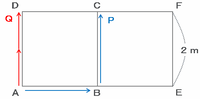
次の図の青い矢印は点Ｐの動きを、そして赤い矢印は点Ｑの動きを表しています。
この図を見れば分かるように、２つの点は辺ＡＤ上を同時に進むときは反対向きにすれちがい、辺ＢＣ上を同時に進むときはＰがＱを追い越します。
※ 画像はすべて、クリックすると拡大します。
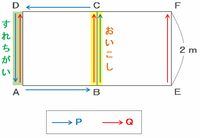
毎秒１ｍで進む点Ｑが初めて辺ＡＤ上を進むのは、スタートからの２秒間です。
ただし、そのときは点Ｐ(毎秒２ｍ)が次の図のように頂点ＡからＣまでしか進めないので、２つの点がすれちがうことはありません。
次に点Ｑが辺ＡＤ上を進むのは、スタートから６秒後に頂点ＦからＡへとワープしてからの２秒間です。
点Ｐは１秒間に正方形ＡＢＣＤの辺を１本ずつ進むので、スタートから６秒後には頂点Ｃにいます。
したがって、次の図のようにスタートから６秒後から８秒後の間に、２つの点は辺ＡＤ上のどこかで初めてすれちがうことになります。
※ ここからは計算に分数が出てくるので、求め方を画像に変換します。
(２)
ＰがＱに追いつく形で出会うのは、２つの点が辺ＢＣ上を同時に進んでいるときです。
点Ｑが初めて辺ＢＣ上を進むのは、頂点ＤからＢへワープした２秒後から４秒後の間です。
ただし、そのときは次の図のように点ＰがＣからＡへ進んでいるので、２つの点が辺ＢＣ上で出会うことはありません。
点Ｑが次に辺ＢＣ上を進むのは、８秒後から１０秒後の間です。
スタートしてから８秒後の点Ｐは、正方形ＡＢＣＤをちょうど２周して頂点Ａにいるので、１０秒後には次の図のようにＣへ進んでいます。
以上から、点Ｐが初めてＱに追いつくのは、スタートから１０秒後になります。
(３)
点Ｐは４秒ごとに頂点Ａへ、そして点Ｑは６秒ごとに頂点Ａへ戻るので、４と６の最小公倍数である１２秒ごとにスタートと同じ状態になります。
２つの点がすれちがうときも１２秒おきにやってくるので、１０回目のすれちがいは１回目のときから１２×９＝１０８秒後になります。
※ ここからは計算に分数が出てくるので、求め方を画像に変換します。
PR
