次の図は、まこと君とたろう君の２人が、ある規則が繰り返されるような並べ方で白と黒の碁石を並べたものです。図のように、１番目から①、②、③、・・・と番号を付けていくとき、次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
まこと君の碁石の列の８６番目は、白・黒どちらですか。
(２)
たろう君の碁石について、１００番目までの白と黒の数を数えたとき、白と黒のどちらが何個多いかを答えなさい。
(３)
２人の並べた列を比べると、７番目や１０番目などのように、※印を付けたところは違う色の碁石が並べられています。このような並び方は１００番目までに何回ありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、まこと君が並べた碁石は「白・黒・白・黒・黒・白・白」の７個が１つのグループになっています。
※ 画像はすべて、クリックすると拡大します。
８６÷７＝１２余り２なので、「白・黒・白・黒・黒・白・白」が１２回繰り返された後、「白・黒」で終わります。
したがって、８６番目の碁石は黒色になります。
(２)
次の図のように、たろう君が並べた碁石は「白・黒・白・黒・黒」の５個が１つのグループになっています。
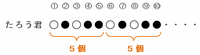
１００÷５＝２０なので、「白・黒・白・黒・黒」をちょうど２０回繰り返して終わります。
５個のグループの中だと黒が白よりも３－２＝１個多いので、それを２０回繰り返すと、黒が１×２０＝２０個多くなります。
(３)
まこと君の並べた碁石は７個ずつ、たろう君の並べた碁石は５個ずつの碁石なので、７と５の最小公倍数である３５個を１つのグループとして考えます。
とりあえず、問題文の図で最初から２０個までの間に色の違う場合が９回あることが分かっているので、残りの２１個目から３５個目までの間に同じようなケースが何回あるのかを確認してみると次の図のようになります。
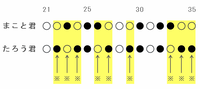
上の図を見れば分かるように、２１番目から３５番目の間で２人の碁石の色が違う場合は９回あります。
つまり、最初から３５個のグループの中で２人の碁石の色が違う場合は９＋９＝１８回あることが分かります。
３５×３＝１０５なので、もし最初から１０５番目まで碁石が並んでいるのなら、２人の碁石の色が違う場合は１８×３＝５４回あるはずです。
ただし、この問題は１００番目までを数えればＯＫなので、最後の５列の中で色違いになる３列分を差し引くと、答えは５４－３＝５１回になります。
【補足】
１０１番目から１０５番目までの碁石の並び方は、３１番目から３５番目の並び方と同じです。
したがって、その中で２人の碁石の色が違うのは３回あることが分かります。
PR
