底面が半径５㎝の円柱の形をした容器が水平な机の上にあり、底面が半径２㎝の円柱の形をしたおもり２個が容器の外に置いてあります。容器の中には水が入っていて、その水の深さと２個のおもりの高さはすべて等しいものとします。次の( )にあてはまる数を求めなさい。ただし、円周率は３.１４とします。
※ 画像はクリックすると拡大します。
(１)
おもりを１個だけ容器の中に入れて、おもりの底面が水平になるように置くと、水の深さは( )倍になります。ただし、水は容器からあふれないものとします。
(２)
次にもう１個のおもりも容器の中に入れ、図Ａのように容器の底面に２個のおもりを並べて置くと、水の深さは３.３㎝になりました。容器に入っている水の量は( )㎤です。
(３)
さらに図Ｂのように、２個のおもりを積み重ねて置くと、水の深さは( )㎝になります。ただし、答えは小数第３位を四捨五入しなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図１のように、おもりを水中に入れる前はおもりの高さと水の深さが同じだったので、それをどちらも「１」とおいてみます。
また、おもりの底面の半径は２㎝、容器の底面の半径は５㎝なので、底面積の比はおもり：容器＝２×２：５×５＝４：２５となります。
※ 画像はすべて、クリックすると拡大します。
このとき、水中に入れるおもりの体積は４×１＝４と表せるので、それが完全に水中へ沈んだとき、水の深さは４÷２５＝０.１６上がります。
※ (水中に入れる物体の体積)÷(容器の底面積)＝水深がどれだけ上がるのか
もともとの容器の水の深さは１、おもりを１個沈めたときにそれが０.１６深くなるので、水の深さは次の図２のように、最初に比べて１＋０.１６＝１.１６倍になります。
(２)
さっきの問題で、おもり１個を水中に沈めると水の深さが０.１６上がることが分かりました。
次の図３のようにおもり２個を沈めた場合、水の深さは最初に比べて０.１６×２＝０.３２上がるので、容器の水深は１＋０.３２＝１.３２と表せます。
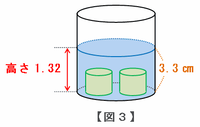
つまり最初の水の深さを１とおくと、その１.３２が３.３㎝にあたるので、おもりを入れる前の水の深さは３.３÷１.３２＝２.５㎝になることが分かります。
容器の底面は半径５㎝なので、容器に入っている水の量は５×５×３.１４×２.５＝１９６.２５㎤になります。
(３)
水中に入れる物体が水面よりも上に飛び出る場合は、
① まずは容器に入っている水をすべて他の場所へ移しておく。
② 空になった容器に物体を入れ、そのときの底面積を求めてみる。
③ 他の場所に移しておいた水を再び容器に入れる。
④ 「水の体積÷②で求めた底面積」を計算して、水の深さを求める。
という流れで答えを求めます。
そこで、まずはおもりと容器の底面積をそれぞれ確認しておくと、
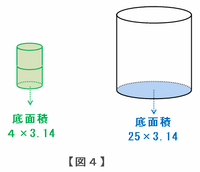
・おもりの底面積→２×２×３.１４＝４×３.１４
・容器の底面積→５×５×３.１４＝２５×３.１４
となります。
※ どちらも「×３.１４」を計算しない理由は後で分かりますが、もしこの時点で「×３.１４」まで計算したとしても普通に答えは求められます。
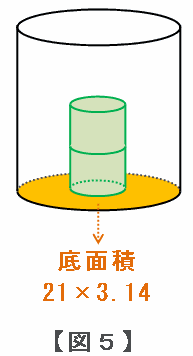
次は図５のように、空の容器におもりを２個入れてみると、容器の中の底面積は２５×３.１４－４×３.１４＝２１×３.１４㎠に減ります。
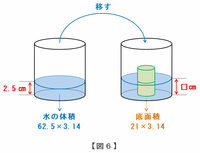
水の体積はさっきの問題で確認したのですが、こちらも「×３.１４」をする前の状態に戻しておくと、５×５×３.１４×２.５＝６２.５×３.１４㎤と表せます。
つまり、この問題は次の図６のように６２.５×３.１４㎤の水を底面積が２１×３.１４㎠の容器に入れたときの水の深さを求めればＯＫなので、「水の体積÷容器の底面積」を計算すれば答えが求められます。
というわけでさっそく計算してみると、(６２.５×３.１４)÷(２１×３.１４)＝６２.５÷２１＝２.９７６・・・となるので、答えは２.９８㎝になります。
【補足】
この最後の割り算で「×３.１４」を約分みたいに消してしまうのがちょっとカッコいいテクニックなわけです(笑)
「×３.１４」はなるべく最後まで残しておくのがポイントですが、この問題に限って言えば、最後の割り算さえ間違えなければどちらでもいいかな？という気がしないでもないです。
PR
