次の図Ａのような、一辺が５個の正方形の形に置いた碁石を、図Ｂのように、たての列の個数がＡと同じになるように並べかえます。すると図Ｂは、たての列が３列と余り１個となります。同じように、一辺が５個以上の正方形の形に置いた碁石を並べかえたときの余りの個数のことを「端数」と呼ぶことにします。図Ｂの場合は、「端数が１」となるわけです。このとき、次の各問いに答えなさい。それぞれ考え方と計算も書きなさい。
※ 画像はクリックすると拡大します。
(１)
一辺が６個の正方形を並びかえたときの端数を求めなさい。
(２)
端数が４となるときの碁石の総数を求めなさい。
(３)
碁石の総数は、「(端数)×( ア )＋( イ )」で求めることができます。この( ア )と( イ )にあてはまる数をそれぞれ求めなさい。
【問題文の追記】
この方法は「薬師算」と呼ばれ、江戸時代に書かれた和算書「塵却記」に載っているものです。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
たとえば１辺に碁石が５個並んでいる場合、普通は次の図１のように５－１＝４個ずつ４か所のグループに分けます。
※ 画像はすべて、クリックすると拡大します。
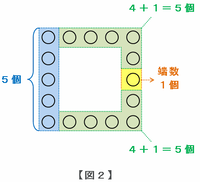
もし１グループの数と１辺に並ぶ碁石の数をそろえたい場合は、次の図２のように、
① まずは左のたて１列に並ぶ５個の碁石を青色の枠で囲む。
② 上段と下段にある４＋１＝５個もそれぞれ緑色の枠で囲む。
③ 最後に残った黄色い部分が端数の碁石となる。
という流れから、１辺に碁石が５個並んでいる場合、端数の碁石は１個であることが分かります。
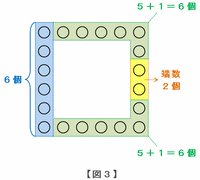
というわけで、次の図３を利用して１辺に碁石が６個並んだ正方形の場合の端数を求めてみると・・・
① まずは左のたて１列に並ぶ６個の碁石を青色の枠で囲む。
② 上段と下段にある５＋１＝６個もそれぞれ緑色の枠で囲む。
③ 最後に残った黄色い部分が端数の碁石となる。
という流れから、１辺に碁石が６個並んでいる場合、端数の碁石は２個になります。
(２)
１辺が５個と６個のときの正方形を次の図４のようにもう一度見直してみると・・・
・１辺が５個の正方形→端数の１個が上下左右に１か所ずつ＋４すみに３個ずつ
・１辺が６個の正方形→端数の２個が上下左右に１か所ずつ＋４すみに３個ずつ
となっています。
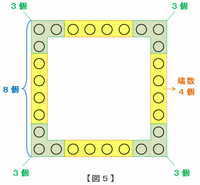
つまり端数が４個の場合は、次の図５のように「上下左右に４個ずつ」と「４すみに３個ずつ」という形で碁石が並んでいるので、碁石は全部で４×４＋４×３＝２８個になります。
(３)
これまでの流れから分かるように、碁石を正方形のように並べた場合は、
・端数の□個が上下左右に１か所ずつ→合わせて□個×４
・４すみにはいつでも碁石が３個ずつ→合わせて４×３＝１２個
という形になっています。
つまり、碁石の総数を求める式は「(端数)×４＋１２個」と表すことができるので、( ア )には４、( イ )には１２がそれぞれあてはまります。
【補足】
そもそも薬師算というのは、
・正方形に並んだ碁石の総数は「(端数)×４＋１２個」で求められる。
・１２といえば薬師如来さまの十二神将でしょ。
という流れでその名がつけられたそうです。
ありがたやありがたや・・・(-人-)
PR
