次の図１のように、はじめに１から８までの数字が１６個のマスにかいてあります。これらの数字を次の【操作】によってかきかえていきます。
【操作】
・Ａ行とＣ行の８個のそれぞれの数字に５をたす。２けたの数になる場合は、その数から１０を引く。
・Ｂ行とＤ行の８個のそれぞれの数字に６をたす。２けたの数になる場合は、その数から１０を引く。
例えば【操作】を１回行うと、図２のようになります。
※ 画像はクリックすると拡大します。
図２において、Ｂ行Ｂ列の数字は「２」、Ｃ行Ｃ列の数字は「１」にかきかえられ、合計は３になります。このとき、次の各問いに答えなさい。
(１)
操作を５回行った後のＢ行Ｂ列の数字とＣ行Ｃ列の数字の合計はいくつになりますか。
(２)
操作を９９回行った後のＢ行Ｂ列の数字とＣ行Ｃ列の数字の合計はいくつになりますか。
(３)
操作を何回か行った後、１６個のマスにかかれているすべての数字の合計が６６で、Ａ行Ａ列の数字が１となりました。このとき、Ｂ行Ｂ列の数字とＣ行Ｃ列の数字の合計はいくつになりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは次の図を利用してＢ行Ｂ列とＣ行Ｃ列の数の規則性を確かめてみると、
・Ｂ行Ｂ列・・・「２→８→４→０→６」の５個がくり返される
・Ｃ行Ｃ列・・・「１→６」の２個が繰り返される
となっています。
※ 画像はすべて、クリックすると拡大します。
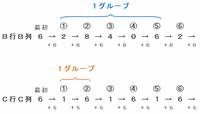
上の図から、操作を５回行った後のＢ行Ｂ列は６、Ｃ行Ｃ列は１になっていることが分かるので、合計は６＋１＝７になります。
(２)
さっき確認したように、Ｂ行Ｂ列の数字は「２→８→４→０→６」の５個がひたすら繰り返されます。
９９÷５＝１９余り４なので、操作を９９回行った後のＢ行Ｂ列は「２→８→４→０→６」の４番目である「０」になります。
Ｃ行Ｃ列の数字は「１→６」の２個がくり返されます。
９９÷２＝４９余り１なので、操作を９９回行った後のＣ行Ｃ列は「１→６」の「１」になります。
以上から、答えは０＋１＝１になります。
(３)
Ａ行Ａ列の数字は１回の操作ごとに「６→１→６→１→・・・」と変化していくので、Ａ行Ａ列の数字が１になったということは、数字を足す操作を偶数回行ったことが分かります。
また次の表のように、Ａ行とＣ行は２個の数字のくり返し、そしてＢ行とＤ行は５個の数字のくり返しなので、その最小公倍数である２×５＝１０回目の操作までを調べれば、合計が６６になるときが必ず見つかるはずです。
※ 下の表の「①」は１回目の操作後の数字、「②」は２回目の操作後の数字があてはまることを表しています。
上の表を見れば分かるように、Ａ行とＣ行は必ず２回目の操作のときの合計が使われます。
２回目の操作後はＡ行が「１・５・８・４」、Ｃ行が「３・７・６・２」なので、その合計は１＋５＋８＋４＋３＋７＋６＋２＝３６になります。
つまり、Ｂ行とＤ行の合計が６６－３６＝３０になるときを見つければＯＫなので、ここからは地道にＢ行とＤ行の１～５回目の合計をそれぞれ求めてみると、次の図のようになります。
つまり、すべてのマス目の数の和が６６になるのは、Ａ行とＣ行が２回目の操作後の数、そしてＢ行とＤ行の数が３回目の操作後の数になるときです。
※ 次の表のように８回目の操作後のとき。
８回目の操作後の図は次のようになるので、Ｂ行Ｂ列とＣ行Ｃ列の合計は４＋６＝１０になります。
PR
