１×２×３×４×・・・と順に整数をかけていくとき、初めて２で１０回割り切れるのは( ア )までかけたときで、初めて１０で１０回割り切れるのは( イ )までかけたときです。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(ア)の求め方
カンタンに言うと、１×２×３×４×・・・と順に整数をかけていく途中で、
・２の倍数を１個使う→２で１回割れるようになる
・２×２＝４の倍数を１個使う→２で２回割れるようになる
・２×２×２＝８の倍数を１個使う→２で３回割れるようになる
という流れになっています。
そこで、次の図のように２から偶数だけを並べてみると、１２まで来たときに、２で割れる回数が１＋２＋１＋３＋１＋２＝１０回になることが分かります。
※ 画像はすべて、クリックすると拡大します。
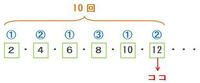
以上から、( ア )にあてはまる数は１２になります。
(イ)の求め方
１×２×３×４×・・・と順に整数をかけていく途中で、
・(２の倍数)×(５の倍数)が１組できる→１０で１回割れるようになる
・(４の倍数)×(２５の倍数)が１組できる→１０で２回割れるようになる
という仕組みになっているので、まずは次の図のように５の倍数だけを小さい順に並べてみます。
上の図を見れば分かるように、５の倍数を４５まで並べたときに、１０で割れる回数がちょうど１０回になります。
以上から、( イ )にあてはまる数は４５になります。
【補足】
１から小さい順に整数を並べたとき、「２の倍数」は「５の倍数」よりもたくさん出てきます。
したがって、(２の倍数)×(５の倍数)の組み合わせを数えるときには、５の倍数がいくつあるのかを確認すればＯＫです。
PR
