気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
05/23
Sun
2010
横浜女学院2010【5】 ☆角度・折り曲げる☆
図1の四角形ABCDは1辺が10㎝の正方形です。それぞれの辺の真ん中の点を、E、F、G、Hとします。次の操作1から操作3まで順番に行います。また、1度折ったところは広げないものとします。このとき、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
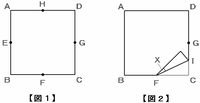
※ 画像はクリックすると拡大します。
(操作1)
図2のように、FCを、FとGを結んだ線に重なるように折ります。
(1)
図2の角Xの大きさは何度ですか。
(操作2)
操作1で折った線と、DC上の交わった点をIとし、IGもFとGを結んだ線に重なるように折ります。
(2)
操作1で折った線と操作2で折った線で作られる角のうち、大きい方の角度は何度ですか。
(操作3)
正方形の他の3つのすみでも、操作1、操作2と同様の折り方をします。
(3)
操作3まで行ったときにできた図形で、紙が重なっていないところの面積は何㎠ですか。
※ 解説を見る場合は、下の「解説はこちらから」をクリック!
(1)
次の図アの三角形GFCは、辺FC=辺GC、角GCF=90度の直角二等辺三角形なので、角GFCと角FGCの大きさはどちらも45度です。
したがって、角Xの大きさは45÷2=22.5度になります。
(2)
このとき次の図オのように、(操作1)でできた赤い折り目である辺FIと、(操作2)でできた青い折り目である辺KGによって、図のような緑色とオレンジ色の2つの角ができるのですが、ここでは大きい方の角度である角FKGの大きさを求めます。
次の図カの角GFKは角Xのことなので、(1)で求めた22.5度です。
以上から、求める角FKGの大きさは180-22.5×2=135度になります。
(3)
2つの操作を終えた後、この正方形の右下(一辺5㎝の正方形)は次の図キのようになっています。
・ピンク色の部分→操作1で紙が重なった部分
・緑色の部分→操作2で紙が重なった部分
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
