下の表は、あるクラスの児童４０人の算数と国語の点数をまとめたものです。表の中の黄色い「１」は算数の得点が８１～９０点、国語の点数が４１～５０点の児童が１人いることを表しています。
※ 画像はクリックすると拡大します。
(１) 表の青い部分には同じ数が入ります。その数は何ですか。
(２) 国語の点数より算数の点数のほうが、確実に高いと読み取れる児童は何人ですか。
(３) 次のア、イ、ウのどれかにあてはまる児童は、必ず放課後に残って勉強をします。そのような児童は何人以上何人以下だと考えられますか。
ア 算数が４０点以下
イ 国語が４０点以下
ウ 合計点が１００点未満
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは表の１行ずつの人数の合計を求めて横に書き込んでみると、次のような図になります。
※ 画像はすべて、クリックすると拡大します。
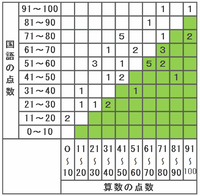
このとき、表の青い２か所を除いた人数の合計は２＋１＋３＋６＋６＋４＋２＋４＋２＝３０人なので、青い２か所で合わせて４０－３０＝１０人いるはずです。
したがって、青い枠にあてはまる数は１０÷２＝５になります。
(２)
国語よりも算数の点数が確実に高い人を数えるためには、
・算数が９１～１００点→国語は８１～９０点、７１～８０点、６１～７０点、・・・
・算数が８１～９０点→国語は７１～８０点、６１～７０点、５１～６０点、・・・
・算数が７１～８０点→国語は６１～６０点、５１～６０点、４１～５０点、・・・
といったように、自分の枠よりも１ランク低い枠から数えていけばＯＫです。
そんな感じで問題文の条件にあてはまる枠をオレンジ色で塗りつぶしてみると、次のような図になります。
※ さっきの問題で求めた２か所の「５」のことも忘れずに！
上の表の緑色に塗りつぶされた部分にある数をすべてたすと、２＋３＋５＋２＋１＋１＋２＝１６人になります。
(３)
まずはアとイの条件にあてはまる児童の人数から確認してみます。
アの「算数が４０点以下」にあてはまる枠を青色に塗りつぶすと、次の図のようになります。
次はイの「国語が４０点以下」にあてはまる枠を緑色に塗りつぶしてみると、下のような図になります。
このとき、上の２つの図を重ねてみると次のようになるのですが、下の図の黄色の部分はアとイの両方の条件にあてはまっている児童を表しています。
ここで上の３つの色で塗りつぶされた枠の人数をそれぞれ求めてみると、
・青色の部分(アだけにあてはまる)→１＋３＋１＝５人
・緑色の部分(イだけにあてはまる)→１人
・黄色の部分(アとイの両方にあてはまる)→１＋１＋１＋２＋２＝７人
となるので、アやイにあてはまる人数の合計である５＋１＋７＝１３人は、放課後に残っていることが確定です。
しかし、次の表の茶色と紫色の枠については、それぞれ合計が１００点未満かどうかはっきりとは分かりません。
・茶色の１人→国語と算数の合計が最低で５１＋４１＝９２点、最高で６０＋５０＝１１０点
・紫色の２人→国語と算数の合計が最低で４１＋４１＝８２点、最高で５０＋５０＝１００点
したがって、この茶色と紫色の枠にあてはまる１＋２＝３人が、ウの「合計点が１００点未満」に全員あてはまる場合、放課後に残る児童は１３＋３＝１６人まで増えます。
以上から、放課後に残る児童の数は１３人以上１６人以下になります。
PR
