Ｓ学院の運動会では、Ａ、Ｂ、Ｃ、Ｄ、Ｅの５チームに分かれて、１５個の競技を順番に行います。各競技の１位は５０点、２位は４０点、３位は３０点、４位は２０点、５位は１０点を獲得し、各競技において同じ順位のチームはないものとします。
１３番目の競技を終えたところでの合計得点は、Ａチームが３９０点、Ｂチームが３８０点、Ｃチームが３５０点でした。ただし、同じ合計得点のチームはなく、１位のチームと２位のチームの得点差は２０点以上あり、１位のチームと５位のチームの得点差は１００点未満でした。このとき、次の問いに答えなさい。
(１)
１３番目の競技を終えたところでの１位のチームの合計得点は何点ですか。
(２)
１４番目の競技ではＡチームが１位になり、１４番目の競技を終えたところでの合計得点は３チームが同じになりました。このとき、その３チームをすべて答えなさい。
(３)
１４番目の競技を終えたところで合計得点が５位だったチームは、１５番目の競技において１位でした。また、Ｄチームは１４番目の競技の順位と１５番目の競技の順位が同じで、Ｅチームも１４番目の競技の順位と１５番目の競技の順位が同じでした。この結果、ある２チームの最終の合計得点が同じになりました。その２つのチームと得点を答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
１３番目の競技までの総得点は(５０＋４０＋３０＋２０＋１０)×１３＝１９５０点、そしてＡ、Ｂ、Ｃ３チームの１３番目の競技を終えた時点での得点の合計は３９０＋３８０＋３５０＝１１２０点なので、ＤチームとＥチームの得点は合わせて１９５０－１１２０＝８３０点になっています。
また、１位と２位の得点差は２０点以上なので、その２つにＡチームとＢチームをあてはめることはできません。
したがって次の図のように、少なくとも１位にはＤチームかＥチームのどちらかが来ることが分かります。
※ 画像はすべて、クリックすると拡大します。
問題はＤチームとＥチームで８３０点をどう分けるのかですが・・・
・２０点差にする→１位が(８３０＋２０)÷２＝４２５点となり、１の位が「０」でないのでダメ
・３０点差にする→１位は４３０点、２位が４００点。１位から５位まで同じ得点のチームがないのでＯＫ
・４０点差にする→１位が４３５点となり、１の位が「０」でないのでダメ
・５０点差にする→１位は４４０点、２位が３９０点。２位がＡチームと同点なのでダメ
・６０点差にする→１位が４４５点となり、１の位が「０」でないのでダメ
・７０点差にする→１位は４５０点、３位が３８０点。１位と５位の得点差が１００点以上になるのでダメ
となることから、ＤチームとＥチームの得点はどちらかが４３０点で１位、そしてもう一方のチームは４００点で２位となることが分かります。
※ どちらのチームが１位なのかは分かりません。
以上から、１位のチームの得点は４３０点になります。
(２)
１４番目の競技でＡチームは１位だったので、合計得点が３９０＋５０＝４４０点になります。
また、さっきの問題で１位がＤチームとＥチームのどちらなのかが結局分からなかったので、とりあえず次の図のように、１３番目の競技が終わった時点の順位を「１位＝Ｄチーム」、「２位＝Ｅチーム」として話を進めていきます。
14番目の競技を終えた時点で３チームの合計得点を同じにするには、次の図のようにＤが４３０＋１０＝４４０点、Ｅが４００＋４０＝４４０点になればＯＫです。
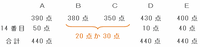
以上から、合計得点が同じ３チームはＡ、Ｄ、Ｅになります。
(３)
１４番目を終えた時点でのＢチームとＣチームの合計得点は、
・Ｂチーム→３８０＋２０＝４００点、または３８０＋３０＝４１０点
・Ｃチーム→３５０＋２０＝３７０点、または３５０＋３０＝３８０点
となることから、４位はＢチーム、そして５位はＣチームであることが分かります。
したがって、１５番目の競技で１位になったのはＣチームなので合計は３７０＋５０＝４２０点、または３８０＋５０＝４３０点になります。
また、ＤチームとＥチームはそれぞれ１５番目の競技の得点が１４番目の競技のときと同じなので、Ｄチームの得点は４４０＋１０＝４５０点、Ｅチームの得点は４４０＋４０＝４８０点になります。
PR
