次の図のように、ア～オまで４つの区間に分けられた全長５００㎞の道があります。この道を、太郎君はアからオへ、花子さんはオからアへ向かって車で同時に出発しました。どちらの車も、晴れの区間は毎時６０㎞、雨の区間は毎時４０㎞で進みます。２人は５時間後に出会いました。また、ア～イの区間の距離は１２０㎞です。太郎君は、出発してから４時間後にウに到着しました。次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) 太郎君と花子さんが出会ったのは、アから何㎞のところですか。
(２) エ～オの区間の距離は何㎞ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
アからイまでの１２０㎞は晴れているので、太郎君が時速６０㎞で進むと１２０÷６０＝２時間かかります。
また、アを出発した太郎君がウに到着したとき４時間が経過していたので、太郎君はイからウまでを４－２＝２時間で進みました。
イからウまでは雨なので、太郎君はその２時間を時速４０㎞で進んだはずです。
したがって、イからウまでは次の図のように４０×２＝８０㎞離れています。
※ 画像はすべて、クリックすると拡大します。
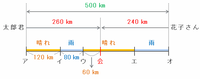
２人はアとオを同時に出発してから５時間後に出会ったので、太郎君は上の図のウからエへ向けてあと５－４＝１時間進めます。
ウからエは晴れているので、その１時間で太郎君は６０×１＝６０㎞進みます。
つまり次の図のように、２人が出会った地点はアから１２０＋８０＋６０＝２６０㎞離れています。
【補足】
上の説明は「２人はウとエの間で出会った」ことを前提として話を進めていますが、多少カンの鋭い子だと「もしかしたらウとエの間がすごく短くて、エとオの間で会ったかもしれないじゃん」と思ったりするわけです。
というわけで、念のためにその可能性も考えてみると、
・太郎君がウまでの２００㎞を進んだ時点で４時間経過してたことは確定。
・もし２人がエとオの間で出会ったのなら、花子さんは５時間ずっと雨の中を進んだ。
・その場合、花子さんが進んだ距離は４０×５＝２００㎞。
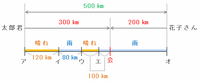
・次の図のように、その地点はアからだと５００－２００＝３００㎞。
・つまり、太郎君は残りの１時間で３００－２００＝１００㎞進んだことになる。
・でも太郎君の速さは晴れでも時速６０㎞。１時間で１００㎞進むとか絶対にムリ。
なので、２人がエとオの間で会うことは絶対にありえません。
(２)
さっきの問題で分かったことをカンタンにまとめると、
・花子さんはずっと雨だと５時間で２００㎞しか進めない。
・花子さんが実際に進んだ距離は５００－２６０＝２４０㎞。つまり雨と晴れの区間が混ざってた。
・じゃあ、晴れの区間をどれぐらい増やせばＯＫなのかな？
となります。
つまり次の図のように、「雨の区間は時速４０㎞」と「晴れの区間は時速６０㎞」という２つのものが混ざり、その合計距離も合計時間も分かっているので、つるかめ算の公式を利用して、雨の区間(つまりオからエ)を進んだ時間を求めることができます。
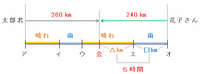
上の図のオからエの区間を走った時間を求めるために、まずは「５時間すべて晴れのときの速さである時速６０㎞で進んだら」と仮定してつるかめ算をスタートします。
もし５時間ずっと晴れていたら、花子さんは６０×５＝３００㎞進みます。
しかし実際に進んだ距離は２４０㎞なので、つるかめ算の公式を利用して時速４０㎞で進んだ時間を求めると、(３００－２４０)÷(６０－４０)＝３時間となります。
つまり、花子さんはオからエまでを時速４０㎞で３時間進んだので、その距離は４０×３＝１２０㎞になります。
PR
