なみさんは分速１８０ｍで家から自転車で学校に向かっていました。信号のところまで来たとき、忘れ物に気づき、先ほどよりもはやい速さで引き返したところ、なみさんが引き返したと同時に家から追いかけ始めたお姉さんと３０秒後に出会いました。忘れ物を受け取ってから、そのままの速さで学校に向かい、３分５０秒後に学校に着きました。そのため、忘れ物をしないで分速１８０ｍで学校に向かったときと同じ時間に着くことができました。
(１)
なみさんが忘れ物に気づいて引き返してからの速さは分速何ｍですか。
(２)
お姉さんが追いかけ始めた速さは分速２００ｍでした。家から学校までは何ｍありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
今日のなみさんは信号の地点で引き返し、次の図のようにＡ地点で姉と出会ってから学校へ向けてまた進み始めます。
したがって、今日のなみさんはＡ地点から学校まで３分５０秒かけて進みました。
※ 画像はすべて、クリックすると拡大します。
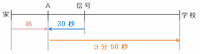
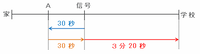
今日のなみさんは信号からＡ地点まで引き返すのに３０秒かかったので、次の図のようにＡ地点から信号まで戻るときにも３０秒かかるはずです(同じ速さだから)。
したがって、今日のなみさんは信号から学校までを３分５０秒－３０秒＝３分２０秒かけて進んだことが分かります。
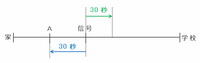
「いつものなみさん」と「今日のなみさん」の進み方を次の図のように比べてみると、今日のなみさんが信号からＡ地点まで引き返す３０秒間に、いつものなみさんは学校へ向けて分速１８０ｍで３０秒間進みます。
その後は今日のなみさんがＡ地点から学校まで進むのにかかる時間と、いつものなみさんが学校までの残りの距離を進むのにかかる時間がどちらも３分５０秒だったので、結局は次の図のように学校へ到着する時間が同じになりました。
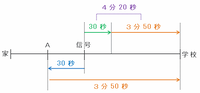
つまり上の図を見れば分かるように、いつものなみさんは信号から学校までの距離を３０秒＋３分５０秒＝４分２０秒かけて進みます。
いつものなみさんと今日のなみさんが信号から学校まで進むのにかかる時間の比は、いつも：今日＝４分２０秒：３分２０秒＝２６０秒：２００秒＝１３：１０になります。
また、時間の比の逆比は速さの比になるので、いつものなみさんと今日のなみさんの速さの比は１０：１３です。
このとき、速さの比の１０がなみさんのいつもの速さである分速１８０ｍにあたるので、比の１は１８０÷１０＝分速１８ｍになります。
今日のなみさんの速さは比の１３なので、答えは１８×１３＝分速２３４ｍです。
(２)
次の図のように、家から信号までは「分速２００ｍの姉」と「分速２３４ｍのなみさん」が向かい合わせで３０秒＝０.５分かけて進んだので、その距離は(２００＋２３４)×０.５＝２１７ｍです。
また、信号から学校までは分速１８０ｍのなみさんが４分２０秒＝３分の１３分かけて進むので、その距離は１８０×３分の１３＝７８０ｍです。
したがって、家から学校までの距離は２１７＋７８０＝９９７ｍになります。
PR
