Ａ地点からＢ地点に行く途中にＰ地点があり、Ａ地点からＰ地点に向かうときは上り坂、Ｐ地点からＢ地点に向かうときは下り坂です。花子さんは、下り坂は上り坂の２倍の速さで歩きます。花子さんがＡ地点からＢ地点に向かって歩いたところ、６０分かかりました。その後、Ｂ地点からＡ地点に向かって歩いたところ、４５分かかりました。Ａ地点からＰ地点までの道のりは、Ｐ地点からＢ地点までの道のりの何倍ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
花子さんは下り坂を上り坂の２倍の速さで進むので、速さの比は上り：下り＝１：２です。
また、花子さんが同じ距離を上りの速さと下りの速さで進んだときにかかる時間の比は、上り：下り＝２：１になります。
※ 速さの逆比は時間の比。
花子さんが次の図の矢印アとイの順に進むと６０分、矢印ウとエの順に進むと４５分かかるので、花子さんはＡＢ間の往復に６０＋４５＝１０５分かかります。
※ 画像はすべて、クリックすると拡大します。
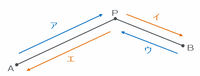
次の図のように「アとウ(上りだけ)」と「イとエ(下りだけ)」の順に進んでもＡＢ間を往復したことになるので、この場合にかかる時間の合計もさっきと同じく１０５分です。
また、同じ距離を上りの速さと下りの速さで進んだときにかかる時間の比は２：１なので、１０５分を２：１に比例配分してみると、
・ＡＢ間を上りの速さだけで進んだときにかかる時間→１０５×３分の２＝７０分
・ＡＢ間を下りの速さだけで進んだときにかかる時間→１０５×３分の１＝３５分
となります。
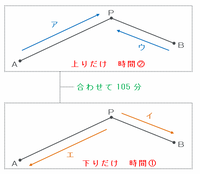
次の図のように、ＡＢ間を上りの速さである①だけで進むと７０分かかるので、ＡＢ間の距離は①×７０＝７０と表せます。
また、普通にＡＰ間を上りの速さ①、ＰＢ間を下りの速さ②で進むと６０分かかるのですが、上りと下りの２つの速さが混ざっていて、ＡＢ間の距離、かかる時間の合計も分かったので、つるかめ算を利用して上りや下りにかかった時間を求めることができます。
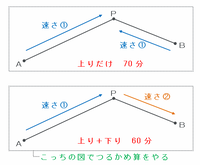
もしＡＢ間を上りの速さである①で６０分間進むと、その距離は①×６０＝６０となります。
しかし、実際の距離は７０なので、つるかめ算の公式を利用して下りにかかった時間を求めると、(７０－６０)÷(②－①)＝１０分間となります。
また、上りを進むのにかかった時間は６０－１０＝５０分間です。
つまり次の図のように、
・ＡＰ間の距離→上りの速さ①で５０分かかるので①×５０＝５０
・ＰＢ間の距離→下りの速さ②で１０分かかるので②×１０＝２０
と表せることが分かったので、ＡＰ間の距離はＰＢ間の５０÷２０＝２.５倍です。
PR
