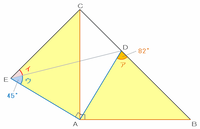
次の図の三角形ＡＢＣと三角形ＡＤＥは直角二等辺三角形で、点Ｄは辺ＢＣ上にあります。
※ 画像はクリックすると拡大します。
(１)
図のアの角が８２度のとき、イの角の大きさを求めなさい。
(２)
ＢＤとＤＣの長さの比が５：３のとき、三角形ＡＤＣと三角形ＥＤＣの面積の比を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図の青い辺ＥＡとＤＡ、オレンジ色の辺ＣＡとＢＡは、どちらも直角二等辺三角形の直角をはさむ２辺なので、それぞれ長さは同じです。
また、「角ＥＡＣ＋ＣＡＤ」と「角ＤＡＢ＋ＣＡＤ」はどちらも９０度なので、角ＥＡＣとＤＡＢの大きさは同じです。
つまり、下の図の三角形ＥＡＣとＤＡＢは「２辺の長さとその間の角の大きさが等しい」ことから合同であり、「角ア」と「角イ＋ウ」の大きさは等しいことが分かります。
※ 画像はすべて、クリックすると拡大します。
次の図の角アは８２度、角ウ(直角二等辺三角形ＡＤＥの内角)は４５度なので、角イの大きさは８２－４５＝３７度になります。
(２)
次の図の辺ＢＤの長さは比の５、ＤＣの長さは比の３なので、辺ＢＣの長さは比の５＋３＝８と表せます。
また、直角二等辺三角形ＡＢＣの頂点Ａから辺ＢＣに向けて垂線を引くと、交点Ｆは辺ＢＣを２等分するので、辺ＦＢの長さは比の８÷２＝４と表せます。
※ ＦＡＢも直角二等辺三角形になるので、辺ＦＡの長さもＦＢと同じく比の４となる。
つまり、三角形ＡＤＣは底辺ＣＤの長さが比の３、高さＦＡが比の４なので、面積は３×４＝１２と表せます(÷２はすべての場合で省略)。
さっきの問題で三角形ＥＡＣとＤＡＢは合同であることが分かったので、次の図の辺ＥＣの長さはＢＤと同じく比の５、そして角ＥＣＡの大きさはＤＢＡと同じく４５度となります。
また、角ＡＣＤは直角二等辺三角形の内角である４５度なので、角ＥＣＤは４５×２＝９０度です。
つまり、下の図のＥＤＣは直角三角形であり、底辺ＥＣの長さが比の５、高さＣＤが比の３なので、面積は５×３＝１５と表せます。
以上から、三角形ＡＤＣの面積は比の１２、三角形ＥＤＣの面積は比の１５と表せることが分かったので、２つの三角形の面積比は１２：１５＝４：５になります。
PR
