１４.４㎞離れたＡ地点からＢ地点へ川が流れています。太郎君はＡからＢへ向かって、次郎君はＢからＡに向かって、それぞれボートで９時に出発しました。９時１５分に２人は初めてすれ違い、その後太郎君は９時２４分にＢへ到着しました。しばらくして、次郎君がＡへ到着したと同時に２人ともそれぞれの地点を折り返しました。その後２人はＡとＢの真ん中で再びすれ違い、同時にＡ、Ｂへ到着しました。静水上の太郎君のボート、次郎君のボートはそれぞれ一定の速さで、川の流れる速さもつねに一定とします。このとき、次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) ２人が初めてすれ違ったのはＡ地点から何㎞離れていますか。
(２) 次郎君がＡ地点へ到着するのは何時何分ですか。
(３) 川の流れの速さは分速何ｍですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次のグラフを見れば分かるように、太郎君はＡからＢまでの１４.４㎞＝１４４００ｍを２４分間かけて下りました。したがって、太郎君が川を下るときの速さは１４４００÷２４＝分速６００ｍです。
※ 画像はすべて、クリックすると拡大します。
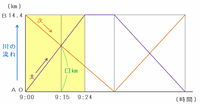
求めたいのは太郎君が１５分間で進んだ距離(上のグラフの□㎞)なので、答えは６００×１５＝９０００ｍ＝９㎞になります。
(２)
次のグラフのように、２人が初めて出会うまでの１５分間で、次郎君は１４４００－９０００＝５４００ｍ進みました。
したがって、次郎君がＢからＡへ川を上るときの速さは５４００÷１５＝分速３６０ｍになります。
次郎君がＢからＡへ進むのにかかる時間は１４４００÷３６０＝４０分なので、答えは９時４０分になります。
(３)
９時４０分に出発した２人がＡＢ間の真ん中ですれ違ったということから、太郎君が川を上るときの速さと次郎君が川を下るときの速さは等しいことが分かります。
PR
