０でない２つの整数ａとｂに対して、ａ☆ｂはａ＋ｂ＋ａ×ｂの値を表します。たとえば３☆４＝１９となります。また、ａ☆ｂ＝１９となる２つの整数ａとｂの組は全部で４組あります。次の問いに答えなさい。
(１) ７３☆５６を求めなさい。
(２) ａ☆ｂ＝３５となるような２つの整数ａとｂの組は全部で何組ありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
問題文に書かれているルールの通り、普通に計算して答えを求めます。
７３☆５６は７３＋５６＋７３×５６＝４２１７になります。
(２)
大まかに言うと、「かけ算(たて×横)の答えは長方形の面積になる」ことを利用して、ａとｂにあてはまる数の組み合わせを見つけてみます。
【３☆４が１９となる理由】
３☆４は「３＋４＋３×４」と変換できるので、次の図の「３」と「４」と「３×４」を合体させれば答えが求められます。
※ 画像はすべて、クリックすると拡大します。
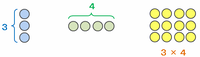
この３つの部品を合体させてみると、次の図アのように長方形から左上が欠けた形ができます。
そこで、図イのように左上に○を１個付け足してやると、たての○は３＋１＝４個、横の○は４＋１＝５個となるので、長方形全体の○は４×５＝２０個になります。
ただし、そのうちの１個は後から付け加えたものなので、３☆４の答えは２０－１＝１９になります。
「なんでそんなややこしい求め方をしなきゃいけないの？」と思うかもしれませんが、この「１個足せば長方形ができる」という話が分からないと問題をスムーズに解くことができないので、もうちょっとだけガマンしてください(笑)
【ａ☆ｂ＝１９となるａとｂの組み合わせを求める】
ａ☆ｂは「ａ＋ｂ＋ａ×ｂ」と変換できるので、次の図のように「ａ」と「ｂ」と「ａ×ｂ」を合体し、さらに左上に○を１個付け足して長方形を完成させてみます。
すると、たての長さは「ａ＋１」、横の長さは「ｂ＋１」となるので、長方形の面積を求める式は(ａ＋１)×(ｂ＋１)と表せます。
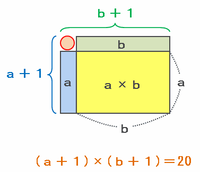
このとき、(ａ＋１)×(ｂ＋１)の答えは１９＋１＝２０となる(赤い○を１個付け足した分だけ合計が１増える)ので、(ａ＋１)×(ｂ＋１)の組み合わせを見つけるには、かけ算の答えが２０となる場合を考えればＯＫであることが分かります。
かけ算の答えが２０となるのは「１×２０」、「２×１０」、「４×５」の３組ありますが、「１×２０」だとａ＋１＝１のときにａが０となってしまうのでダメです。
そこで「２×１０」と「４×５」のときにａやｂがいくつになるのかを確認してみると、
① (ａ＋１)×(ｂ＋１)＝２×１０のとき
・ａ＋１＝２なので、ａは２－１＝１となります。
・ｂ＋１＝１０なので、ｂは１０－１＝９となります。
② (ａ＋１)×(ｂ＋１)＝４×５のとき
・ａ＋１＝４なので、ａは４－１＝３となります。
・ｂ＋１＝５なので、ｂは５－１＝４となります。
という流れになるので、(ａ・ｂ)は(１・９)、(３・４)の２組と、それらの数字をひっくり返してできる(９・１)、(４・３)の合わせて４組であることが分かります。
※ ａ☆ｂ＝１９のａとｂの組み合わせが４組できることは問題文に書いてあります。
はい、前置きが長くて申し訳ありませんでした(笑)ここからいよいよ本題でございます・・・
【ａ☆ｂ＝３５となるａとｂの組み合わせを求める】
ａ☆ｂ＝ａ＋ｂ＋ａ×ｂの式をさっきと同じように長方形に変換してみると、次の図のように(ａ＋１)×(ｂ＋１)の答えは３５＋１＝３６となります。
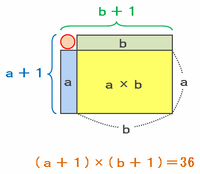
かけ算の答えが３６となるのは「１×３６」、「２×１８」、「３×１２」、「４×９」、「６×６」の５組ありますが、「１×３６」だとａ＋１＝１のときにａが０となってしまうのでダメです。
そこで、残りの４組のときにａやｂがいくつになるのかを確認してみると、次の①～④のようになります。
① (ａ＋１)×(ｂ＋１)＝２×１８のとき
・ａ＋１＝２なので、ａは２－１＝１となります。
・ｂ＋１＝１８なので、ｂは１８－１＝１７となります。
② (ａ＋１)×(ｂ＋１)＝３×１２のとき
・ａ＋１＝３なので、ａは３－１＝２となります。
・ｂ＋１＝１２なので、ｂは１２－１＝１１となります。
③ (ａ＋１)×(ｂ＋１)＝４×９のとき
・ａ＋１＝４なので、ａは４－１＝３となります。
・ｂ＋１＝９なので、ｂは９－１＝８となります。
④ (ａ＋１)×(ｂ＋１)＝６×６のとき
・ａ＋１＝ｂ＋１＝６なので、ａとｂはどちらも６－１＝５となります。
これらの組み合わせのうち、①～③はａとｂの数が違うので数字をひっくり返してもう１組ずつ作ることができますが、④はａとｂが同じ数なのでひっくり返すことができません。
以上から、ａとｂの組み合わせは全部で３×２＋１＝７組できます。
【補足】
その７組を全部書き出してみると、(ａ・ｂ)＝(１・１７)、(１７・１)、(２・１１)、(１１・２)、(３・８)、(８・３)、(５・５)となります。
PR
