１０００ｍはなれたＡ地点とＢ地点の間を普通列車と快速列車が運行します。普通列車と快速列車の速度の比は３：７、長さの比は２：３です。
今、Ａ地点から普通列車の先頭が、Ｂ地点から快速列車の先頭が同時に出発します。どちらの列車もＡ、Ｂ地点に列車の最後尾が着いた瞬間に逆方向に折り返し、運行し続けます。このとき次の問いに答えなさい。
(１)
２つの列車が初めて出会うのはＡ地点から何ｍのところか求めなさい。
(２)
２つの列車が初めて出会ったところからＡ地点に２０ｍ近いところですれ違い終わりました。このとき普通列車の長さは何ｍであるか求めなさい。
(３)
(２)のとき、普通列車が出発してからＡＢ間を１２往復する間に快速列車は何往復するか求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
速さの比は同じ時間に進む距離の比と等しいので、普通列車と快速列車が出会うまでに進む距離の比は次の図のように３：７になっています。
※ 画像はすべて、クリックすると拡大します。
つまり、ＡＢ間の１０００ｍを３：７に比例配分すれば普通列車と快速列車が出会うまでに進んだ距離をそれぞれ求めることができるので、２つの列車が初めて出会ったのは、Ａ地点から１０００×(１０分の３)＝３００ｍです。
(２)
普通列車(長さ２)と快速列車(長さ３)の先頭が出会ってからすれ違い終わるまでの様子を図に表すと次のようになります。
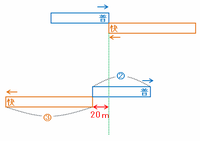
上の図で普通列車が進んだ距離は、普通列車の長さである②よりも２０ｍ少ないので「②－２０ｍ」と表すことができます。
一方、快速列車は③よりも２０ｍ多く進んだので「③＋２０ｍ」と表せます。
２つの列車が同じ時間(すれ違っているとき)に進む距離の比は普通：快速＝３：７なので、「②－２０ｍ」と「③＋２０ｍ」の比が３：７であることが分かります。
比は外項と内項の積が等しいので、「②－２０ｍ」の７倍と「③＋２０ｍ」の３倍をそれぞれ求めてみると、
・「②－２０ｍ」の７倍→(②－２０ｍ)×７＝⑭－１４０ｍ
・「③＋２０ｍ」の３倍→(③＋２０ｍ)×３＝⑨＋６０ｍ
となるので、「⑭－１４０ｍ」と「⑨＋６０ｍ」は次の図のように長さが等しくなります。
上の図の⑭－⑨＝⑤が６０＋１４０＝２００ｍにあたるので、比の①は２００÷⑤＝４０ｍだと分かります。
普通列車の長さは比の②にあたるので、答えは４０×②＝８０ｍになります。
※ 快速列車の長さは比の③なので、４０×③＝１２０ｍです。
(３)
次の図のように、普通列車はＡＢ間を行きと帰りに１０００＋８０＝１０８０ｍずつ進むので、ＡＢ間を１２往復したときに進んだ距離は１０８０×２×１２＝２５９２０ｍになります。
また、普通列車の速さは３なので、その距離を進むのにかかる時間は２５９２０÷３＝８６４０と表せます。
快速列車の速さは７なので、８６４０の時間で進む距離は７×８６４０＝６０４８０ｍと表せます。
次の図のように、快速列車はＢＡ間を行きと帰りに１０００＋１２０＝１１２０ｍずつ進むので、ＢＡ間を１往復したときに進む距離は１１２０×２＝２２４０ｍになります。
以上から、普通列車がＡＢ間を１２往復する８６４０の時間で、快速列車はＢＡ間を６０４８０÷２２４０＝２７往復します。
PR
