図は、兄と弟が正午に自宅を出発して、１２㎞はなれた駅に着くまでの道のりと時間の関係を表したグラフです。兄は、途中で速さを２倍にして駅に向かいました。弟は、自宅から５㎞の地点で速さを２倍にして家にもどり、休けい後、自宅にもどった速さの１.２５倍の速さで出発しました。その後、駅まで残り２㎞の地点で３０分間休けいし、再び駅に向かったところ、兄と同時に駅に着きました。次の問いに答えなさい。
※ 画像はクリックすると拡大します。
(１) 兄と弟が駅に着いた時刻は午後何時何分ですか。
(２) 兄と弟が最初に出会った時刻は午後何時何分ですか。
(３) 弟が自宅で休けいした時間は何分間ですか。
(４) 兄と弟が２回目に出会ってから３回目に出会うまでの時間は何分間ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
２人は同時に出発して同時に着いたので、速さが１度しか変わらなかった兄の進み方を利用してかかった時間を求めればＯＫです。
次のグラフのように、兄は最初の４.５㎞＝４５００ｍを９０分かけて進んだので、そのときの速さは４５００÷９０＝分速５０ｍになります。
※ 画像はすべて、クリックすると拡大します。
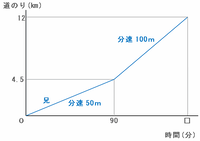
兄の後半の速さは５０×２＝分速１００ｍ、残りの距離は１２０００－４５００＝７５００ｍなので、兄が残りの距離を進むのにかかる時間は７５００÷１００＝７５分です。
つまり、兄は家から駅まで９０＋７５＝１６５分＝２時間４５分かかったので、この兄弟が駅に着いた時刻は午後２時４５分になります。
(２)
２人が最初に出会うのは、下のグラフの赤い印がつけられた時間です。
弟は最初の５㎞＝５０００ｍを５０分かけて進んだので、そのときの速さは５０００÷５０＝分速１００ｍです。
その後は速さを２倍にしたので、５０分後からは１００×２＝分速２００ｍで進みます。
また、兄はスタートから５０分間で５０×５０＝２５００ｍ進むので、５０分後の２人は５０００－２５００＝２５００ｍ離れています。
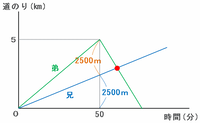
２人は５０００ｍ離れた地点から向かい合わせで進むので、出会うまでにかかる時間は２５００÷(５０＋２００)＝１０分になります。
つまり、２人は自宅を出発してから５０＋１０＝６０分＝１時間後に初めて出会うので、そのときの時刻は午後１時になります。
(３)
弟が自宅で休けいしていたのは、下のグラフの赤い部分の時間です。
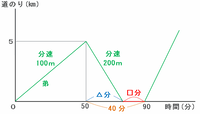
分速２００ｍで進む弟が家までの５０００ｍを戻るのにかかる時間は、５０００÷２００＝２５分です。
それが上のグラフの青い△分にあたるので、弟は９０－５０＝４０分間のうち、４０－２５＝１５分間休けいしていたことになります。
(４)
２人が２回目に出会うのは下のグラフのオレンジ色の印のとき、そして３回目に出会うのは赤色の印のときです。
まずは旅人算の公式を利用して、下のグラフの「□分」と「△ｍ」にあてはまる数を求めてみます。
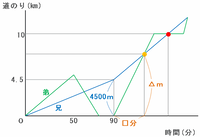
２人が自宅を出発してから９０分後、兄は弟よりも４５００ｍ先を分速１００ｍで進んでいます。
ここからは弟の速さが２００×１.２５＝分速２５０ｍになるので、その距離の差を追いつくまでにかかる時間は４５００÷(２５０－１００)＝３０分になります。
また、その間に弟は自宅から２５０×３０＝７５００ｍ進んだので、３回目に出会う地点までの残りの距離は１００００－７５００＝２５００ｍになります。
これまでに分かったことを下のようにグラフに書き込んでみると、２人が２回目から３回目に出会うまでにかかる時間は、兄が２５００ｍ進むのにかかる時間と等しいことが分かります。
※ 求めたいのは下のグラフの「？分」にあてはまる時間です。
以上から、２人が２回目に出会ってから３回目に出会うまでにかかる時間は、２５００÷１００＝２５分間になります。
PR
