２地点Ａ、Ｂがあります。太郎さんと花子さんはＡを同時に出発し、Ｂに向かってそれぞれ一定の速さで走り、ＡＢ間を何度も往復します。太郎さんは花子さんより速く走ります。グラフは太郎さんと花子さんのへだたり(距離)と時間のようすを表したものです。このとき、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
グラフの①と②の時間を求めなさい。
(２)
太郎さんが花子さんを初めて追い越すのは、出発してから何分何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは次のグラフ１にあるア～カのときの２人の動きを確認してみると、
・ア→太郎さんが初めてＢに到着してＡへ折り返し
・イ→ＢからＡへ向かう太郎さんとＡからＢへ向かう花子さんがすれ違い
・ウ→花子さんが初めてＢに到着してＡへ折り返し(太郎さんはＡへ向かう途中)
・エ→太郎さんがＡに到着してＢへ折り返し(花子さんはＡへ向かう途中)
・オ→ＡからＢへ向かう太郎さんとＢからＡへ向かう花子さんがすれ違い
・カ→太郎さんが再びＢに到着してＡへ折り返し(花子さんはＢへ向かう途中)
となっています。
※ 画像はすべて、クリックすると拡大します。
ただ、上のようなグラフだと１本の線しかなくて読み取るのが大変なので、２人がＡＢ間を往復する様子を下のグラフ２のように書きかえてみます。
このグラフ２を見れば分かるように、太郎君はＡＢ間を４２秒間で１往復しています。
グラフ２の①は太郎君がＡＢ間を片道分だけ進むのにかかる時間を表しているので、①には４２÷２＝２１秒があてはまります。
また、この２人が２回目に出会ったのは太郎さんが折り返してから４８－４２＝６秒後なので、１回目に出会うのは次のグラフのように太郎さんが折り返してから６÷２＝３秒後になります。
このグラフのアは２１秒後なので、２人が１回目に出会ったのはスタートしてから２１＋３＝２４秒後になります。
２人が１回目に出会うまでの様子を線分図に表してみると次のようになります。
太郎さんはＡＢ間を２１秒で進み、折り返して３秒後に花子さんと出会ったので、太郎さんはＡ地点から出会った地点までを２１－３＝１８秒で進むことが分かります。
つまり、Ａ地点から出会った地点までの距離とＢ地点から出会った地点までの距離の比は１８：３＝６：１になります。
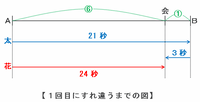
花子さんは上の図の６の距離を２４秒かけて進んだので、Ｂ地点までの残り１の距離を進むのに２４÷６＝４秒かかります。
グラフの②には花子さんがＡＢ間を進むのにかかった時間があてはまるので、答えは２４＋４＝２８秒になります。
(２)
さっきの問題で、ＡＢ間を太郎さんは２１秒、花子さんは２８秒かけて進むことが分かったので、２人が同じ距離を進むのにかかる時間の比は太郎：花子＝２１：２８＝３：４になります。
また、時間の逆比は速さの比なので、２人の速さの比は太郎：花子＝４：３になることも分かります。
太郎さんが花子さんを初めて追いぬくためには、次の図のように太郎さんが花子さんよりも１往復分だけ多く進めばＯＫです。
太郎さんが花子さんを追いぬくまでに進んだ距離の比は太郎：花子＝④：③なので、その差の①がＡＢ間の１往復分にあたります。
①がＡＢ間１往復分なら④はＡＢ間４往復分にあたるので、太郎さんがＡＢ間の４往復分の距離を進んだときに初めて花子さんを追いぬきます。
太郎君はＡＢ間の１往復に４２秒かかるので、４往復するのにかかる時間は４２×４＝１６８秒＝２分４８秒になります。
PR
