生徒の宿泊で、１室の定員を５人ずつにすると全部の部屋を使っても４人分足りなくなり、１室の定員を６人ずつにすると５人の部屋が１室ずつでき、１室が余ります。このときの生徒の人数を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
よくあるタイプの過不足算とこの問題との違いをカンタンに確認しておくと、
・普通の過不足算→たくさんの人間がモノ(あめとかえんぴつとか)を欲しがっている
・この問題の場合→たくさんの部屋が人間を欲しがっている
という感じになります。
そこで、まずは問題文を人間ではなく部屋の気持ちになって読み直してみます。
【１つ目の条件を読み直してみる】
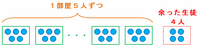
「１室の定員を５人ずつにすると全部の部屋を使っても４人分足りない」とあることから、すべての部屋に生徒が５人ずつ収まった後、次の図のようにまだ生徒が４人余っていることが分かります。
※ 画像はすべて、クリックすると拡大します。
【２つ目の条件を読み直してみる】
「１室の定員を６人ずつにすると５人の部屋が１室ずつでき、１室が余ります」とあることから、各部屋に生徒を６人ずつ収めていくと、次の図のように「生徒が６－５＝１人足りない部屋」と「生徒が６人足りない部屋」が１つずつできることが分かります。
ここまでの流れをふまえて問題文の２つの条件を過不足算っぽく書きかえてみると・・・
・１つ目の条件→生徒を部屋に５人ずつ配ると、生徒が４人余る。
・２つ目の条件→生徒を部屋に６人ずつ配ると、生徒が１＋６＝７人足りない。
となるので、過不足算の公式を利用して部屋の数を求めると、(４＋７)÷(６－５)＝１１室になります。
※ (余り＋不足)÷(配る数の差)＝部屋に化けたくれくれ星人の数
したがって、生徒の人数は５×１１＋４＝５９人になります。
PR
