たての長さが２㎝、横の長さが４㎝の長方形のタイルＡと、１辺の長さが３㎝の正方形のタイルＢがそれぞれ何枚かあります。Ａ、Ｂすべてのタイルの面積の和は１７２㎠で、Ａ、Ｂすべてのタイルの周の長さの和は２４０㎝です。Ａ、Ｂはそれぞれ何枚ありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずはタイルＡとＢそれぞれの面積と周りの長さを求めてみると、
・タイルＡ→面積は２×４＝８㎠、周りの長さは(２＋４)×２＝１２㎝
・タイルＢ→面積は３×３＝９㎠、周りの長さは３×４＝１２㎝
となることから、この２つのタイルは周りの長さがどちらも１２㎝であることが分かります(次の図参照)。
※ 画像はクリックすると拡大します。
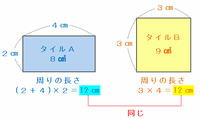
Ａ、Ｂすべてのタイルの周の長さの和は２４０㎝なので、この２種類のタイルは合わせて２４０÷１２＝２０枚あります。
つまり、２種類のタイルの面積と枚数の合計が分かったので、つるかめ算の公式を利用してそれぞれのタイルの枚数を求めることができます。
【タイルＡの枚数を求めるつるかめ算】
タイルＢ１枚の面積は９㎠なので、もし２０枚のタイルが全部Ｂだったら、面積の合計は９×２０＝１８０㎠です。
しかし、実際の面積の合計は１７２㎠なので、つるかめ算の公式を利用してタイルＡの枚数を求めると、(１８０－１７２)÷(９－８)＝８枚になります。
また、タイルＢの枚数は２０－８＝１２枚です。
【タイルＢの枚数を求めるつるかめ算】
タイルＡ１枚の面積は８㎠なので、もし２０枚のタイルが全部Ａだったら、面積の合計は８×２０＝１６０㎠です。
しかし、実際の面積の合計は１７２㎠なので、つるかめ算の公式を利用してタイルＢの枚数を求めると、(１７２－１６０)÷(９－８)＝１２枚になります。
また、タイルＡの枚数は２０－１２＝８枚です。
PR
