Ａ小学校の６年生は９６人で、テストの平均点は７６点でした。Ｂ小学校とＣ小学校の６年生の人数の比は９：７で、２校のテストの平均点は８７点でした。Ａ、Ｂ、Ｃの３校のテストの平均点は８４点でした。Ｂ小学校の６年生の人数を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
テストの平均点を食塩水の濃度、６年生の人数を食塩水の重さにおきかえると、天びん図を利用して問題を解くことができます。
「平均７６点のＡ小学校の生徒９６人」と「平均８７点のＢ小学校とＣ小学校の生徒□人」を混ぜ合わせると、全体の平均点が８４点になるので、次の図のように
・天びん図の左側→平均点の低いＡ小学校の平均点と人数
・天びん図の右側→平均点の高いＢ小学校とＣ小学校の平均点と人数
を書きこみます。
※ 画像はすべて、クリックすると拡大します。
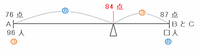
上の図の左のうでの長さは８４－７６＝８点、右のうでの長さは８７－８４＝３点なので、うでの長さの比は左：右＝８：３です。
また、うでの長さの逆比が人数の比にあたるので、「Ａ小学校」と「Ｂ小学校＋Ｃ小学校」の人数の比は３：８となります。
つまり、Ａ小学校の６年生である９６人が比の③にあたるので、比の①は９６÷③＝３２人、そしてＢ小学校とＣ小学校の６年生の合計である比の⑧は３２×⑧＝２５６人であることが分かります。
次の図のように、Ｂ小学校とＣ小学校の６年生の人数比は９：７なので、比の９＋７＝１６が２５６人にあたります。
つまり、２５６人を９：７に比例配分すればＢ小学校とＣ小学校それぞれの６年生の人数が求められるので、Ｂ小学校の６年生の人数は２５６×１６分の９＝１４４人になります。
【補足】
今回は天びん図を利用して「Ｂ小学校＋Ｃ小学校」の６年生の人数を求めましたが、普通は次の図のような面積図を使って解くのかなー、とも思ったりします。
※ たての長さが点数、横の長さが人数を表しています。
上の図のイがアの部分に流れ込んだ結果、３つの学校の平均点が８４点になるので、アとイの面積は同じです。
つまり、「アの横の長さ×８」と「イの横の長さ×３」の答えが等しいので、アとイの横の長さ(ＡとＢＣの人数)の比は３：８となります。
PR
