春子と夏子がゲームをしています。１回ごとに、勝った人の持ち点には１０点を加え、負けた人の持ち点からは４点を引きます。
(１)
２人とも最初の持ち点が１９０点でゲームを始め、１８回ゲームをしたとき、春子が３００点になりました。春子は何勝何敗ですか。
(２)
２人とも最初の持ち点が３１０点でゲームを始めました。夏子が６００点になったとき、夏子の勝った回数は、負けた回数よりも８回多くなりました。夏子は何勝何敗ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
もし１８回のゲームすべてに勝つと得点が１０×１８＝１８０点増えるはずですが、そこから１回負けるごとに、
・勝つともらえるはずだった１０点がもらえなくなる。
・負けるとペナルティとして４点引かれる。
ので、次の図のように１０＋４＝１４点ずつ減っていきます。
※ 画像はすべて、クリックすると拡大します。
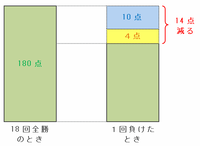
１８回のゲームを終えたとき、春子さんの得点は３００－１９０＝１１０点増えました。
つまり、春子さんの得点の増え方は、１８回全勝のときに比べて１８０－１１０＝７０点少ないので、７０÷１４＝５回負けたことが分かります。
春子さんが勝った回数は１８－５＝１３回なので、答えは１３勝５敗になります。
【補足】
たとえば「１個８０円のトマトと１個５０円のピーマンを合わせて２０個買ったら・・・」のような普通のつるかめ算の場合、トマトとピーマンを１個交換するたびに、合計金額は８０－５０＝３０円ずつ変わっていきます。
しかしこの問題の場合、勝ちと負けを１回交換するたびに、合計得点は１０－４＝６点ではなく、１０＋４＝１４点ずつ変わっていきます。
足すのか引くのかの違いはあるものの、「１回交換すると合計がいくつずつ変わっていくのか」を手掛かりにすることは同じなので、この問題もつるかめ算の仲間と言えます。
(２)
夏子さんの得点が６００－３１０＝２９０点増えるまでの勝った回数と負けた回数を線分図に表すと次のようになります。
勝った回数は負けた回数より８回多いので、その分で１０×８＝８０点増え、残りの２９０－８０＝２１０点は、勝ち負けが同じ回数ずつの部分で増えました。
このゲームは勝つと１０点もらえ、負けると４点引かれるので、１勝１敗をくり返すと、次の図のように得点は１０－４＝６点ずつ増えていきます。
つまり、夏子さんは１勝１敗ペースでゲームを続けて６点ずつ稼いでいったら２１０点増えたので、１勝１敗を２１０÷６＝３５セットくり返したことが分かります。
以上から、夏子さんは２１０点増やすために３５勝３５敗して、残りの８０点を稼ぐために８回勝ったことが分かったので、６００点になるまでの成績は４３勝３５敗になります。
PR
