佐藤君と山田君がＡ地点からＢ地点に行くことになり、まず佐藤君がＡを出発し、次に午前１０時に山田君が出発しました。それぞれ一定の速さで歩いていき、２人とも正午に着く予定でした。しかし、山田君は途中のＣ地点から自転車に乗り、進む速さを３倍にしたため、自転車に乗ってから４分後に佐藤君をＥ地点で追い越しました。そして佐藤君が正午にＢ地点に着いたときには、山田君はＢ地点からさらにＡＢ間と同じ距離にあるＤ地点まで進んでいました。
(１)
ＡＣの距離とＣＢの距離の比、ＣＥの距離とＥＢの距離の比、山田君の自転車の速さと佐藤君の歩く速さの比をそれぞれ求めなさい。ただし、できるだけ簡単な整数の比で答えなさい。
(２)
(１)で求めたことを用いて、佐藤君がＡ地点を出発した時刻を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
【ＡＣの距離とＣＢの距離の比の求め方】
山田君が自転車で進むときの速さは歩くときの３倍なので、歩くときの速さを①とおくと、自転車で進むときの速さは③となります。
最初の予定では、山田君はＡ地点を１０時に出発し、Ｂ地点まで①の速さで歩いて１２時に到着するはずでした。
つまり、次の図のＡＢ間は、①の速さで２時間＝１２０分進んだ距離にあたるので、①×１２０＝２４０と表せます。
※ 画像はすべて、クリックすると拡大します。
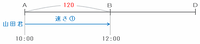
しかし実際には、次の図のように途中のＣ地点から自転車に乗って速さ③で進んだので、１２時にはＤ地点まで進んでいました。
また、図のＢＤ間はＡＢ間の距離と等しいので、Ａ地点からＤ地点までの距離は１２０×２＝２４０と表せます。
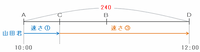
上の図は２つの速さが混ざっていて、時間の合計(１２０分)も距離の合計(２４０)も分かっているので、速さのつるかめ算を利用して、山田君がＡＣ間を歩いて進むのにかかった時間を求めることができます。
山田君が１２０分間をすべて速さ③で進むと、そのときの距離は③×１２０＝３６０になります。
しかし、実際のＡＤ間の距離は２４０なので、つるかめ算の公式を使って速さ①で進んだ時間を求めると、(３６０－２４０)÷(③－①)＝６０分になります。
つまり次の図のように、速さ①で進む山田君は、
・予定だとＡＢ間を進むのに１２０分かかる。
・実際にはＡＣ間を６０分かけて進んだ。
ことから、ＣＢ間も同じ速さで進むと１２０－６０＝６０分かかることが分かります。
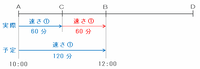
つまり、ＡＣ間とＣＢ間はどちらも同じ距離なので、距離の比は１：１になります。
【ＣＥの距離とＥＢの距離の比の求め方】
次の図のＡＣ間は山田君が速さ①で歩いて６０分かかる距離なので①×６０＝６０、そしてＣＢ間はＡＣ間と距離が等しいのでこちらも６０と表せます。
また、ＣＥ間は自転車に乗った山田君が速さ③で４分進んだ距離なので、③×４＝１２となります。
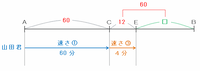
上の図のＥＢ間の距離は６０－１２＝４８なので、ＣＥ間とＥＢ間の距離の比は１２：４８＝１：４になります。
【山田君の自転車の速さと佐藤君の歩く速さの比の求め方】
次の図のＣＥ間とＥＢ間の距離の比は１：４なので、ＡＣ間の距離(ＣＢ間と等しい)は１＋４＝５、そしてＢＤ間の距離(ＡＢ間と等しい)は５×２＝１０と表せます。
また、自転車に乗った山田君がＥ地点で佐藤君に追いついた後、
・山田君→１２時まで自転車でＥＤ間を進んだ。
・佐藤君→１２時まで歩いてＥＢ間を進んだ。
ことも分かります。
つまり、自転車に乗った山田君がＥＤ間の距離である４＋１０＝１４を進む時間で、佐藤君はＥＢ間の距離である４を歩いて進むので、山田君の自転車と佐藤君の歩く速さの比は、１４：４＝７：２になります。
(２)
さっきの問題で、自転車に乗った山田君の速さを７とすると、佐藤君が歩く速さは２と表せることが分かりました。
次の図のＣＥ間は、自転車に乗った山田君が速さ７で４分かけて進んだので、その距離は７×４＝２８となります。
また、その４分間は佐藤君も２の速さで歩いているので、佐藤君が４分間で進む距離は２×４＝８となります。
８の距離を４分で進む佐藤君が、２８の距離を進むのにかかる時間を□分とおくと、８：４分＝２８：□分という比例式ができます。
□には４×２８÷８＝１４分があてはまるので、佐藤君がＣＥ間を歩くと１４分かかることが分かります。
次の図のように、ＣＥ間の距離を１とおくとＡＢ間の距離は１０なので、佐藤君はＡＢ間を進むのに１４×１０＝１４０分＝２時間２０分かかります。
佐藤君がＢ地点に着いたのは１２時なので、Ａ地点を出発した時刻は、１２時－２時間２０分＝午前９時４０分になります。
PR
